‹-- Назад
Координаты векторов
-- 
-мерное линейное пространство, вещественное или комплексное, 
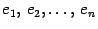
-- базис. Тогда произвольный вектор 
из представим в виде линейной комбинации векторов базиса:
называются координатами вектора в базисе 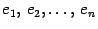. Столбец 
из координат вектора называется координатным столбцом вектора .
Доказательство. Предположим противное. Пусть 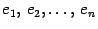-- базис, в котором у вектора есть два различных набора координат:
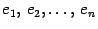
-- линейно зависимы, что противоречит определению базиса. Полученное противоречие означает, что предположение о наличии двух различных наборов координат неверно.
-мерном пространстве задан базис 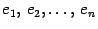. Тогда координатный столбец суммы векторов равен сумме координатных столбцов слагаемых, координатный столбец произведения вектора на число равен координатному столбцу вектора, умноженному на это число. Доказательство. Пусть векторы и 
имеют координатные столбцы и 
соответственно. Отсюда следует, что
Это равенство означает, что координатный столбец вектора
имеет вид 
. Первая часть предложения доказана. Доказательство второй части предоставляем читателю. Из последнего предложения следует, что как только в -мерном пространстве зафиксирован базис, каждый вектор можно заменить его координатным столбцом, и операциям сложения и умножения на число соответствуют такие же операции над их координатными столбцами. Таким образом, каждое -мерное пространство является, с точки зрения алгебры, копией пространства 
в вещественном случае, а в комплексном -- копией 
.
