mathserfer.narod.ru

        Пример 8.5   Найдём стационарные точки функции

заданной на всей плоскости .

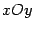
Частные производные функции 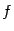равны

В стационарной точке обе эти производные равны 0. Приравнивая полученные выражения к 0, получаем систему линейных уравнений:

Эта система имеет единственное решение: умножая первое уравнение на 2 и вычитая из него второе, получаем , откуда и . Значит,  -- единственная стационарная точка функции .     

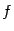
        Пример 8.6   Найдём производную функции

в точке по направлению , составляющему угол с направлением оси .

Из условия следует, что направляющие косинусы оси равны

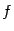
Частные производные функции равняются

Их значение в точке таково:

Для нахождения производной по направлению применяем формулу

Получаем:

    

        Пример 8.7   Найдём производную функции

в точке по направлению , заданному вектором .

Находим единичный направляющий вектор оси :

Поскольку , получаем, что

Найдём теперь градиент: поскольку

и

то

Теперь находим производную по направлению:

    

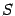
        Пример 8.8   Найдём уравнение касательной плоскости к поверхности , заданной уравнением

в точке

Уравнение касательной плоскости к поверхности в точке имеет вид

Находим частные производные и их значения в точке :

Поэтому искомое уравнение касательной плоскости имеет вид

или

    

        Пример 8.9   Найдём уравнения касательной и нормали, проведённых к линии уровня функции в точке .

Линия уровня задаётся уравнением

Касательная к этой линии уровня имеет вид

а нормаль (напомним, что нормаль -- это прямая, проходящая через точку касания перпендикулярно касательно) можно задать уравнением вида

Вычисляем значения частных производных:

откуда получаем уравнение касательной:

и нормали:

    

        Пример 8.10   Найдём уравнения касательной плоскости и нормали, проведённых к поверхности уровня функции , проходящей через точку .

Найдём уравнение поверхности уровня: поскольку поверхность уровня задаётся уравнением

Это уравнение задаёт эллипсоид вращения (вокруг оси ) с центром в точке и полуосями , и .

Найдём значения частных производных функции 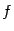в точке :

Записываем уравнение касательной плоскости в виде

то есть

Уравнения нормальной прямой записываем в виде

то есть

    

Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции