‹-- Назад
Евклидово пространство
Вспомним, как в обычном трехмерном пространстве мы вычисляли скалярное произведение векторов. Если координаты векторов
и
-мерном пространстве. Пусть 
-- вещественное -мерное пространство, в котором задан базис 
. Тогда векторы 
и 
из задаются своими координатами:
, задается формулой 
В отличие от обычного трехмерного пространства, где с помощью транспортира и линейки можно измерить угол между векторами и длину вектора, в -мерном пространстве ни угол между векторами, ни длину вектора измерить невозможно (как можно, например, измерить длину многочлена или угол между многочленами?). Поэтому ортонормированным в -мерном пространстве называется тот базис, в котором скалярное произведение вычисляется по формуле (18.3).
Если 
, 
-- координатные столбцы векторов и , то скалярное произведение можно задать формулой
В трехмерном пространстве модуль вектора равен корню квадратному из скалярного произведения вектора на себя 
. В евклидовом пространстве модуль вектора определим аналогично
В трехмерном пространстве с помощью склярного произведения определялся угол между векторами. В евклидовом пространстве тоже можно определить угол между векторами. Но угол в -мерном пространстве не имеет существенного значения, кроме одного случая. В трехмерном проcтранстве два вектора ортогональны тогда и только тогда, когда их скалярное произведение равно нулю.
, их координатные столбцы 
, 
. Проверьте, являются ли векторы ортогональными. Решение. Находим скалярное произведение
Так как базисные векторы имеют координатные столбцы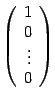 
, 
, ..., 
, то несложно проверить, что в ортонормированном базисе 
, а 
при 
, то есть векторы базиса попарно ортогональны.
Если -- комплексное линейное -мерное пространство, то в нем тоже можно ввести скалярное произведение, задав его формулой
означает комплексное сопряжение.
В унитарном пространстве модуль вектора и условие ортогональности вводятся с помощью скалярного произведения так же, как в евклидовом пространстве. В координатной записи
