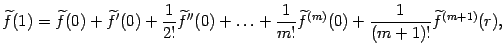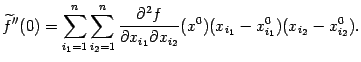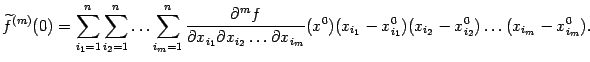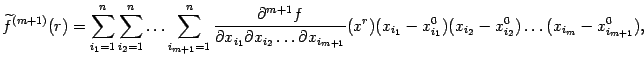‹-- Назад
Вывод формулы Тейлора
Предположим, что в рассматриваемой области
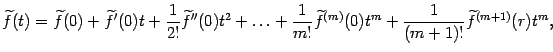 |
где
где
Очевидно, что ![]() . Посмотрим, как производные
. Посмотрим, как производные
Для нахождения ![]() воспользуемся формулой производной сложной функции:
воспользуемся формулой производной сложной функции:
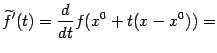 | |
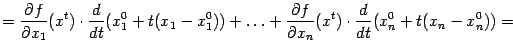 | |
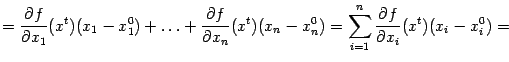 | |
При
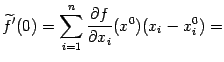 | (9.2) |
| (9.3) |
Вычислим теперь ![]() , для чего найдём
, для чего найдём ![]() :
:
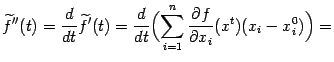 | |
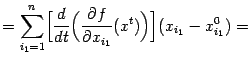 | |
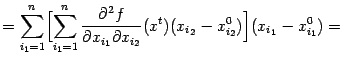 | |
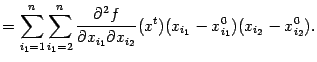 |
Положив в этой формуле
Каждое последующее дифференцирование, как нетрудно понять, будет увеличивать на единицу количество суммирований от 1 до ![]() , порядок частных производных функции
, порядок частных производных функции ![]() , вычисленных в точке
, вычисленных в точке ![]() , а также количество сомножителей-биномов вида
, а также количество сомножителей-биномов вида ![]() . Для третьей производной получаем
. Для третьей производной получаем
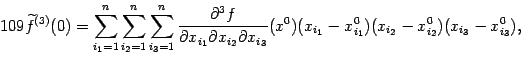 |
а для производной порядка
Правая часть формулы (9.5) содержит
где
Подставляя выражения (9.2), (9.4),..., (9.5), (9.6) в правую часть формулы (9.1), получаем в результате следующее утверждение:
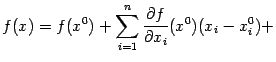 | (9.6*) |
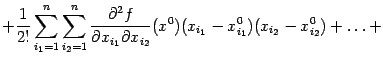 | |
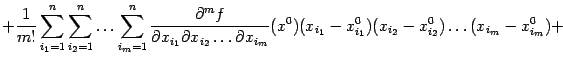 | |
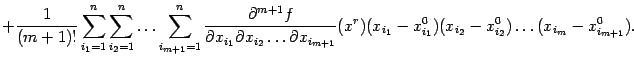 | (9.7) |
Сумма всех слагаемых в правой части формулы (9.6*), кроме записанных в последней строке, называется многочленом Тейлора функции ![]() в точке
в точке ![]() , а эта последняя строка содержит остаточный член формулы Тейлора. Считая его малым при небольших расстояниях между
, а эта последняя строка содержит остаточный член формулы Тейлора. Считая его малым при небольших расстояниях между ![]() и
и ![]() (он имеет порядок
(он имеет порядок ![]() , в то время как все остальные слагаемые -- порядок не выше
, в то время как все остальные слагаемые -- порядок не выше ![]() , если не обращаются в 0), мы можем не учитывать остаточный член и, тем самым, получаем приближённую формулу
, если не обращаются в 0), мы можем не учитывать остаточный член и, тем самым, получаем приближённую формулу
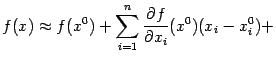 | |
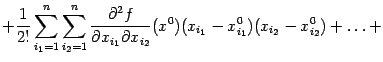 | |
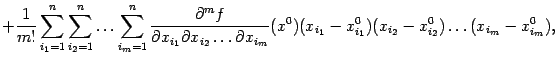 |
содержащую лишь значения функции
При ![]() получается линейное приближение функции
получается линейное приближение функции ![]() (нетрудно видеть, что правая часть совпадает с линейной функцией
(нетрудно видеть, что правая часть совпадает с линейной функцией ![]() , графиком которой служит касательная плоскость, проведённая при
, графиком которой служит касательная плоскость, проведённая при ![]() к графику функции
к графику функции ![]() ):
):
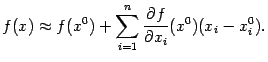 |
При ![]() получается квадратичное приближение функции
получается квадратичное приближение функции ![]() :
:
Многочлен Тейлора в этом случае оказывается многочленом второй степени относительно переменных