‹-- Назад
Пример 9.2 Найдём разложение по формуле Тейлора для функции
в точке
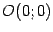
, до слагаемых третьего порядка включительно.
Значение функции в точке 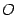 :
:  .
.
Частные производные первого порядка равны
их значения в точке
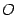
:
Частные производные второго порядка равны
их значения в точке
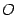
:
Наконец, частные производные третьего порядка равны
их значения в точке
:
Значит, формула Тейлора, учитывающая слагаемые до третьего порядка включительно, такова:
Ответ: 
Пример 9.3 Найдём квадратичное приближение для функции

в окрестности точки

и вычислим приближённо значение выражения

.
Имеем:
Поэтому искомое приближение будет иметь вид
Подставляя сюда  и
и  , получаем:
, получаем:
Ответ: 

С помощью формулы Тейлора можно получать разложение многочленов от переменных  по степеням биномов
по степеням биномов  .
.
Пример 9.4 Найдём разложение многочлена
по степеням биномов

и

.
Для этого разложим функцию  по формуле Тейлора в точке
по формуле Тейлора в точке  . Имеем:
. Имеем:
Все производные порядков 4 и выше тождественно равны 0. Поэтому остаточный член четвёртого порядка в формуле Тейлора будет тождественно равен 0 и мы получаем точное, а не приближённое равенство:
Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции
![]() :
: ![]() .
. 








![]()





![]() и
и ![]() , получаем:
, получаем: ![]()
![]()
![]() по степеням биномов
по степеням биномов ![]() .
. ![]() по формуле Тейлора в точке
по формуле Тейлора в точке ![]() . Имеем:
. Имеем: 




