‹-- Назад
Композиция функций
Если даны два отображения ![]() и
и ![]() , где
, где ![]() , то имеет смысл "сквозное отображение"
, то имеет смысл "сквозное отображение" ![]() из
из ![]() в
в ![]() , заданное формулой
, заданное формулой ![]() ,
, ![]() , которое называется композицией функций
, которое называется композицией функций ![]() и
и ![]() и обозначается
и обозначается ![]() .
.

Рис.1.30.Сквозное отображение  из
из  в
в 
Таким образом, ![]() ,
, ![]() при всех
при всех ![]() . Другое название композиции -- сложная функция (так как сквозное отображение
. Другое название композиции -- сложная функция (так как сквозное отображение ![]() "сложено" из отображений
"сложено" из отображений ![]() и
и ![]() ).
).
Пример 1.18 Пусть  ,
,  , и
, и  ,
,  . Тогда
. Тогда  , и определена композиция
, и определена композиция 
Упражнение 1.3 Покажите, что если заменить множество  в предыдущем примере на
в предыдущем примере на  , то композиция
, то композиция  снова будет определена, но равна теперь
снова будет определена, но равна теперь  , а не
, а не  .
.
Пример 1.19 Пусть  ,
,  , и
, и  ,
,  . Тогда определена композиция
. Тогда определена композиция  , заданная формулой
, заданная формулой  . По известной формуле приведения полученная композиция -- это косинус:
. По известной формуле приведения полученная композиция -- это косинус:  при всех
при всех  .
.
Замечание 1.5 Даже если для функций  и
и 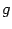 имеют смысл обе композиции
имеют смысл обе композиции  и
и  (что бывает далеко не для любой пары функций
(что бывает далеко не для любой пары функций  и
и 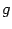 ), то функции
), то функции  и
и  не обязаны совпадать; как правило, это не так.
не обязаны совпадать; как правило, это не так.
Пример 1.20 Пусть  и
и  ,
,  . Тогда
. Тогда  , а
, а  . Очевидно, что это разные функции:
. Очевидно, что это разные функции:  при всех
при всех  , а
, а  принимает значение
принимает значение  , например, при
, например, при  .
.
Применяя композицию функций, которые сами могут получаться как композиции, мы можем получать сложные функции вида ![]() и более длинные композиции.
и более длинные композиции.
Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции