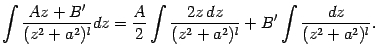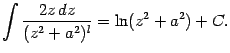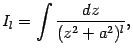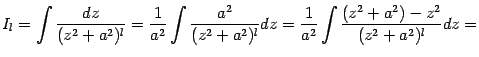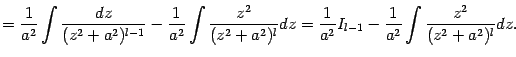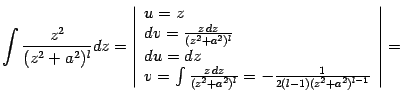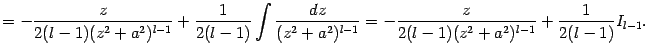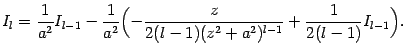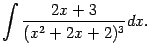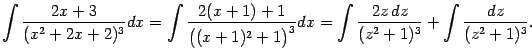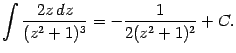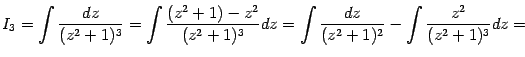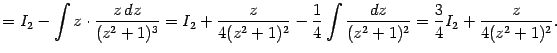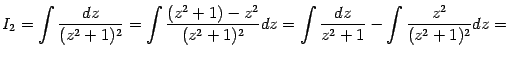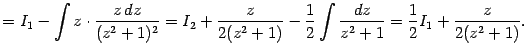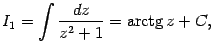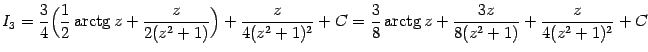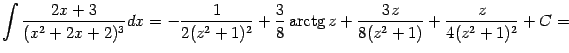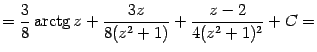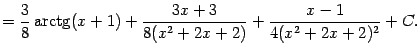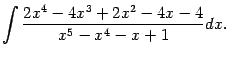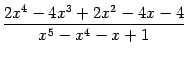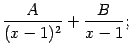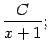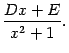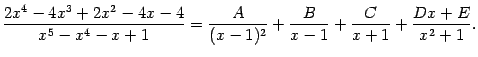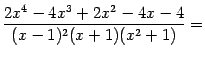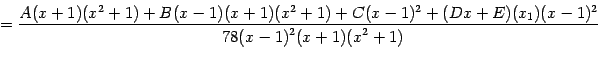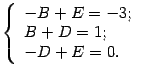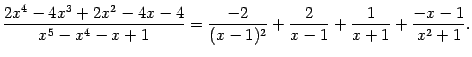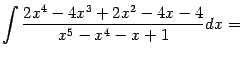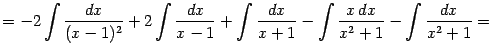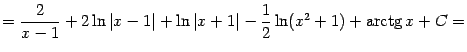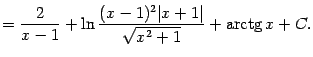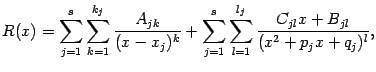‹-- Назад Функция
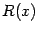
называется
рациональной функцией, или
рациональной дробью, если она представляет собой отношение двух многочленов
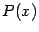
и
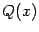
:
Пусть степень многочлена
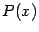
равна
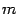
, а степень
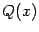
равна
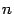
, то есть
где
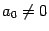
и
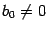
. Разделив числитель и знаменатель на число
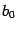
, мы получим, что коэффициент при старшей степени
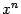
в знаменателе равен 1. Для дальнейшего нам будет удобно предполагать, что эта операция уже произведена, то есть что
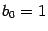
. Далее мы будем предполагать, что все коэффициенты
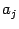
и
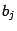
-- вещественные числа.
Если 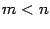 , то дробь
, то дробь 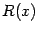 называется правильной, а если
называется правильной, а если 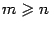 , то неправильной. Если дробь неправильная, то её числитель
, то неправильной. Если дробь неправильная, то её числитель 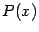 можно поделить на знаменатель
можно поделить на знаменатель 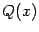 , получив при этом частное
, получив при этом частное 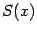 и остаток
и остаток 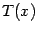 , степень которого
, степень которого 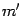 меньше
меньше 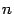 . Это означает, что
. Это означает, что
или что
где
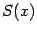
-- некоторый многочлен, называемый
целой частью рациональной дроби
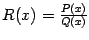
. Если остаток
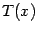
тождественно равен 0, то многочлен
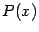
делится на
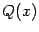
без остатка, и функция
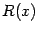
является многочленом, то есть совпадает со своей целой частью
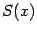
.
С интегрированием целой части дроби 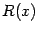 , то есть многочлена
, то есть многочлена 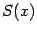 , не возникает никаких проблем, так что в дальнейшем мы можем заняться выяснением способов интегрирования лишь правильных рациональных дробей.
, не возникает никаких проблем, так что в дальнейшем мы можем заняться выяснением способов интегрирования лишь правильных рациональных дробей.
Для нахождения частного 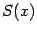 и остатка
и остатка 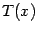 можно применять алгоритм деления многочленов "столбиком". Приведём пример.
можно применять алгоритм деления многочленов "столбиком". Приведём пример.
Пример 2.9 Разделим с остатком
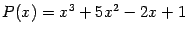
-- многочлен третьей степени -- на бином
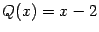
-- многочлен первой степени:
Таким образом, мы представили неправильную рациональную дробь
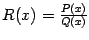
в виде
здесь мы получили частное
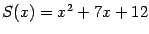
и остаток
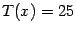
-- многочлен нулевой степени, то есть постоянную.
Знаменатель 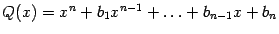 раскладывается в произведение вещественных линейных и квадратичных множителей, то есть имеет вид
раскладывается в произведение вещественных линейных и квадратичных множителей, то есть имеет вид
Линейный множитель
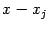
повторяется в разложении
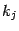
раз, это означает, что вещественное число
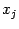
-- корень многочлена
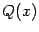
кратности
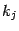
. Относительно квадратичных множителей
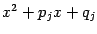
мы будем предполагать, что они не имеют вещественных корней, то есть что их дискриминанты отрицательны:
и корни составляют пару комплексно сопряжённых чисел:
(Здесь и далее
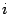
-- мнимая единица, так что
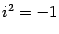
.) Квадратичный множитель
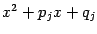
повторяется в разложении
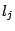
раз; это соответствует тому, что каждое из комплексно сопряжённых чисел
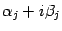
и
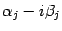
служит
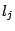
-кратным корнем многочлена
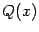
.
Указанное разложение многочлена 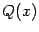 можно выписать, если каким-либо способом отыскать все его корни, как вещественные, так и комплексные, и найти их кратности. Заметим также, что сумма кратностей всех корней равна степени многочлена:
можно выписать, если каким-либо способом отыскать все его корни, как вещественные, так и комплексные, и найти их кратности. Заметим также, что сумма кратностей всех корней равна степени многочлена:
Если найден какой-либо корень 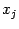 , то это означает, что
, то это означает, что 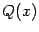 делится на бином
делится на бином 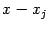 без остатка:
без остатка:
где степень частного
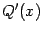
равна
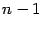
. Точно так же, если найден какой-либо комплексный корень
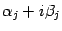
(тогда и сопряжённое число
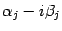
тоже является корнем
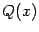
), то
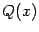
делится без остатка на произведение
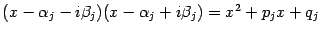
, то есть
где степень частного
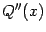
равна
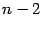
.
Замечание 2.3 Если
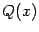
-- многочлен с целочисленными коэффициентами
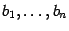
, то, согласно теореме Виета, все целые корни этого многочлена содержатся среди делителей (как положительных, так и отрицательных) свободного члена
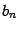
. Проверив все эти делители, мы можем натолкнуться на некоторые из корней; если же ни один из делителей
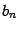
не является корнем
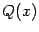
, то это означает, что
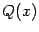
не имеет ни одного целого корня.
Пример 2.10 Разложим на множители многочлен третьей степени
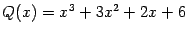
. Проверим, нет ли у него целых корней. Если есть, то этот корень должен быть одним из делителей свободного члена, то есть числа 6. Эти делители равны
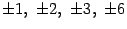
. Подставляем эти числа в
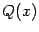
по порядку:
Натолкнулись на корень многочлена, который оказался равным
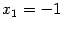
. Значит,
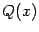
делится без остатка на бином
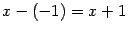
. Выполним это деление "столбиком":
Значит,
Корни частного, то есть квадратного трёхчлена
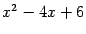
, найдём обычным способом:
Эти два корня оказались комплексными, так что искомое разложение многочлена
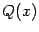
на вещественные линейные и квадратичные множители уже получено: это
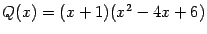
. Кратности как корня
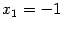
, так и пары корней
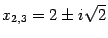
, оказались равными 1.
Итак, предположим, что нам дана правильная рациональная дробь
Её знаменатель
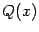
после разложения на множители может содержать множители следующих четырёх видов:
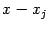
(если кратность корня
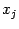
равна 1);
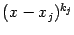
, где
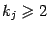
(эти множители соответствуют вещественным корням кратности больше 1);
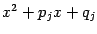
(если кратность комплексных корней
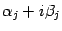
равна 1) и, наконец,
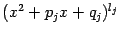
(если кратность комплексных корней
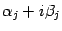
больше 1).
Каждому из указанных типов множителей знаменателя соответствуют простейшие рациональные дроби, а именно:
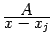 -- простейшая дробь первого типа;
-- простейшая дробь первого типа;
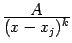 , где
, где 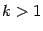 , -- простейшая дробь второго типа;
, -- простейшая дробь второго типа;
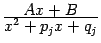 -- простейшая дробь третьего типа;
-- простейшая дробь третьего типа;
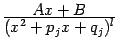 , где
, где 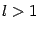 , -- простейшая дробь четвёртого типа.
, -- простейшая дробь четвёртого типа.
Здесь 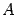 и
и 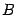 -- некоторые постоянные.
-- некоторые постоянные.
Любая правильная дробь 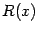 раскладывается в сумму простейших дробей указанных четырёх типов.
раскладывается в сумму простейших дробей указанных четырёх типов.
Если в знаменателе дроби 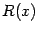 имеется множитель
имеется множитель 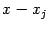 , то разложение будет содержать слагаемое в виде простейшей дроби первого типа
, то разложение будет содержать слагаемое в виде простейшей дроби первого типа 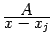 , где
, где 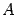 -- некоторое число.
-- некоторое число.
Если имеется множитель 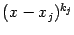 , где
, где 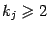 , то разложение будет содержать серию слагаемых, в количестве
, то разложение будет содержать серию слагаемых, в количестве 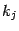 штук, вида
штук, вида 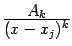 , где
, где 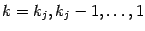 , -- это простейшие дроби второго и (последняя) первого типа. (Следует заметить, однако, что непременно присутствует в разложении лишь слагаемое со старшей степенью, равной
, -- это простейшие дроби второго и (последняя) первого типа. (Следует заметить, однако, что непременно присутствует в разложении лишь слагаемое со старшей степенью, равной 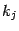 ; может оказаться, что некоторые, или даже все, остальные слагаемые имеют числители
; может оказаться, что некоторые, или даже все, остальные слагаемые имеют числители 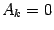 .)
.)
Если в знаменателе имеется множитель 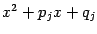 , то разложение будет содержать слагаемое, равное соответствующей простейшей дроби третьего типа,
, то разложение будет содержать слагаемое, равное соответствующей простейшей дроби третьего типа, 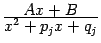 , где
, где 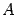 и
и 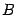 -- некоторые числа.
-- некоторые числа.
Наконец, если имеется множитель 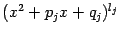 , где
, где 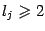 , то разложение будет содержать серию слагаемых, в количестве
, то разложение будет содержать серию слагаемых, в количестве 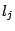 штук, вида
штук, вида 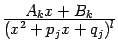 , где
, где 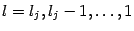 ; -- это простейшие дроби четвёртого и (последняя) третьего типа. В разложении непременно присутствует лишь слагаемое со старшей степенью, равной
; -- это простейшие дроби четвёртого и (последняя) третьего типа. В разложении непременно присутствует лишь слагаемое со старшей степенью, равной 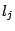 , а остальные слагаемые могут в некоторых случаях оказаться равными 0.
, а остальные слагаемые могут в некоторых случаях оказаться равными 0.
Сказанное можно выразить формулой, дающей разложение правильной дроби в сумму простейших дробей:
где
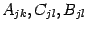
-- некоторые постоянные. Эти постоянные отыскивают
методом неопределённых коэффициентов, выписав разложение (
2.4) в соответствии с видом разложения на множители знаменателя
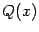
дроби
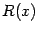
.
Для отыскания неизвестных постоянных методом неопределённых коэффициентов нужно, выписав разложение 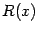 в сумму простейших дробей по формуле (2.4), привести к общему знаменателю сумму, стоящую в правой части. Заметим, что этот общий знаменатель, очевидно, равен
в сумму простейших дробей по формуле (2.4), привести к общему знаменателю сумму, стоящую в правой части. Заметим, что этот общий знаменатель, очевидно, равен 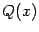 . Получим, что в левой и правой части равенства стоят дроби с одинаковыми знаменателями; значит, и числители у них также тождественно равны. Числитель в правой части содержит неизвестные постоянные
. Получим, что в левой и правой части равенства стоят дроби с одинаковыми знаменателями; значит, и числители у них также тождественно равны. Числитель в правой части содержит неизвестные постоянные 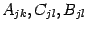 , а числитель левой части -- нет.
, а числитель левой части -- нет.
Далее можно действовать одним из двух способов: либо, воспользовавшись тем, что числители тождественно равны друг другу, подставлять в тот и в другой некоторые "удобные" значения 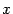 и получать значения постоянных или линейные уравнения, которым они удовлетворяют; либо приравнивать друг к другу коэффициенты при одинаковых степенях
и получать значения постоянных или линейные уравнения, которым они удовлетворяют; либо приравнивать друг к другу коэффициенты при одинаковых степенях 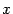 в числителях левой и правой частей: эти коэффициенты также совпадают вследствие тождественности числителей. Это также будет давать линейные уравнения, которым должны удовлетворять неизвестные коэффициенты. Оба описанных способа получения соотношений между коэффициентами можно комбинировать друг с другом так, чтобы найти коэффициенты наиболее удобным способом.
в числителях левой и правой частей: эти коэффициенты также совпадают вследствие тождественности числителей. Это также будет давать линейные уравнения, которым должны удовлетворять неизвестные коэффициенты. Оба описанных способа получения соотношений между коэффициентами можно комбинировать друг с другом так, чтобы найти коэффициенты наиболее удобным способом.
Приведём пример.
Пример 2.11 Разложим рациональную дробь
в сумму простейших дробей и вычислим
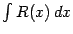
.
Заметим, что в знаменателе этой дроби стоит многочлен 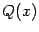 , для которого в предыдущем примере мы нашли разложение на множители:
, для которого в предыдущем примере мы нашли разложение на множители: 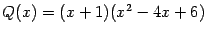 . Поэтому сумма будет состоять из двух слагаемых: простейшей дроби первого типа, соответствующей линейному множителю
. Поэтому сумма будет состоять из двух слагаемых: простейшей дроби первого типа, соответствующей линейному множителю 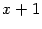 , и простейшей дроби третьего типа, соответствующей квадратичному множителю
, и простейшей дроби третьего типа, соответствующей квадратичному множителю 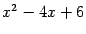 . Итак, вид разложения таков:
. Итак, вид разложения таков:
серия, соответствующая
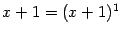
, состоит из 1 слагаемого; серия, соответствующая
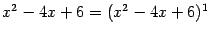
, также содержит только 1 слагаемое. Через
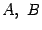
и
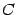
обозначены неизвестные пока постоянные.
Для нахождения этих постоянных приведём правую часть к общему знаменателю:
Поскольку дроби в левой и в правой частях этого равенства тождественно равны и имеют одинаковые знаменатели, то тождественно равны и их числители
3:
Это равенство верно при всех значениях
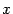
, в том числе и при
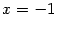
. Подставим
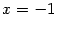
в левую и правую часть равенства и получим:
Последняя скобка равна 0, так что получаем:
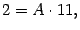
откуда
Других "удобных" значений
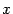
, то есть таких, чтобы какая-либо скобка в правой части обращалась в 0, больше нет, ведь квадратный трёхчлен
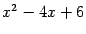
, как мы проверяли ранее, не имеет вещественных корней. Так что далее мы можем либо подставлять "не вполне удобные" значения
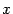
, вроде
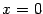
, либо приравнивать друг к другу коэффициенты при одинаковых степенях
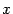
в левой и правой частях. Пойдём комбинированным путём: сначала подставим
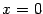
(заметим, что это -- то же самое, что приравнять друг к другу свободные члены левой и правой частей):
Это даёт нам равенство
Поскольку уже известно
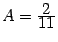
, получаем:
Наконец, приравняем коэффициенты при
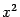
: в левой части коэффициент равен 5, а в правой, после раскрытия скобок, он оказывается равным
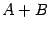
, так что
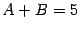
, откуда
Итак, все три неизвестных коэффициента найдены, и получено разложение
Теперь мы можем представить интеграл от дроби 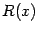 в виде:
в виде:
Интеграл в первом слагаемом -- табличный:
(Здесь и далее
-- уже не найденный выше коэффициент разложения, а произвольное постоянное слагаемое.) В знаменателе дроби во втором интеграле выделим полный квадрат:
и сделаем замену
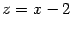
:
Последний интеграл -- табличный:
а в предыдущем интеграле нужно сделать замену
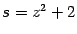
, откуда
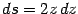
и
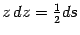
, так что этот интеграл приводится к виду
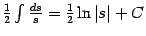
. Итак,
Учитывая, что
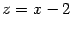
и
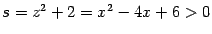
, получаем окончательно:
Замечание 2.4 Если исходная правильная дробь является чётной функцией от
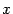
, то есть содержит в числителе и знаменателе
4 одни лишь чётные степени
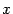
, то и в правой части разложения достаточно оставить одни лишь чётные относительно
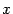
слагаемые. Действительно, если дробь имеет вид
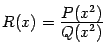
, где
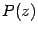
и
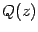
-- многочлены от переменного
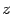
, то мы можем разложить на сумму простейших дробей правильную дробь
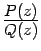
, а потом подставить в каждом из слагаемых разложения
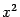
вместо
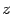
. Очевидно, что тогда все эти слагаемые, зависящие только от
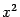
, будут чётными функциями. Например, разложение правильной дроби
следует отыскивать в виде
а не в виде
поскольку слагаемые
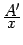
и
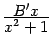
-- нечётные функции от
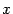
. Тем самым нам надо будет отыскать всего два неизвестных коэффициента
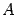
и
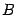
вместо четырёх:
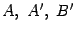
и
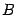
.
Точно так же, в случае когда 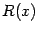 -- нечётная функция от
-- нечётная функция от 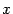 , в искомом разложении можно оставить одни лишь нечётные слагаемые: например, разложение дроби
, в искомом разложении можно оставить одни лишь нечётные слагаемые: например, разложение дроби
следует искать в виде
вместо
сэкономив на поиске чётных слагаемых
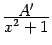
и
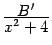
, коэффициенты которых
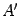
и
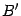
всё равно окажутся равны 0.
Разобранный выше пример 2.11 показывает, что после разложения правильной дроби в сумму простейших дробей интегрирование сводится к интегрированию полученных простейших дробей. Разберём интегрирование всех четырёх типов простейших дробей по порядку.
Интегрирование простейшей дроби первого типа сводится к применению табличной формулы:
Интегрирование простейшей дроби второго типа сводится к табличной формуле после замены вида 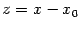 :
:
Интегрирование простейшей дроби третьего типа выполняется с помощью выделения в знаменателе полного квадрата и разбиения интеграла на два слагаемых, которые вычисляются как было показано выше в примере:
где
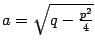
и
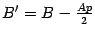
. Осталось подставить
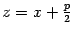
:
Разумеется, заучивать полученную формулу не нужно, а нужно научиться выполнять для конкретных примеров все указанные преобразования.
Интегрирование простейшей дроби четвёртого типа также начинается с выделения в знаменателе полного квадрата и замены 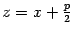 , после чего интеграл
, после чего интеграл 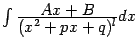 приводится к виду
приводится к виду 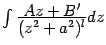 , где
, где 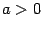 . Разбиваем этот интеграл на два слагаемых:
. Разбиваем этот интеграл на два слагаемых:
Первый из интегралов легко вычисляется заменой
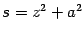
:
Для второго интеграла,
мы можем получить формулу понижения степени, если преобразуем его следующим образом:
Последний интеграл преобразуем, применив формулу интегрирования по частям:
Подставив это выражение в (
2.4*), получаем:
Это и есть формула понижения степени, сводящая вычисление интеграла
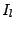
к вычислению интеграла
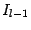
. Если
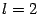
, то интеграл
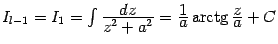
-- табличный; если же
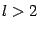
, то для вычисления
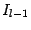
нужно снова применить формулу понижения степени, и так до тех пор, пока не получится тот же табличный интеграл
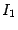
.
Пример 2.12 Вычислим интеграл
Сделав замену
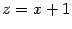
, получаем:
В первом из двух слагаемых сделаем замену
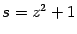
и получим:
Во втором слагаемом применим описанный выше метод понижения степени:
Для вычисления
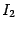
ещё раз применим тот же самый приём:
Поскольку
имеем
и
Приведём теперь пример на интегрирование правильной рациональной дроби общего вида:
Пример 2.13 Вычислим интеграл
Под знаком интеграла -- правильная дробь, поскольку степень числителя, равная 4, меньше степени знаменателя, равной 5. Разложим на множители знаменатель дроби. Это можно сделать, например, группировкой слагаемых:
если учесть, что
Значит, в разложении дроби
в сумму простейших дробей будут получаться следующие серии слагаемых: множителю
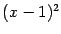
знаменателя будет соответствовать серия из двух слагаемых, второго и первого типа:
множителю
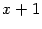
-- одно слагаемое первого типа:
множителю
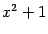
-- одно слагаемое третьего типа:
Итак, ищем методом неопределённых коэффициентов разложение подынтегральной дроби в виде
Приводим правую часть к общему знаменателю. Этот общий знаменатель равен
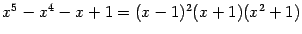
, так что
Поскольку должны быть тождественно равны эти две дроби с одинаковыми знаменателями, приравниваем числители:
Из этого соотношения мы должны найти неизвестные коэффициенты
Для этого сначала используем подстановку "удобных" значений
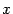
, то есть
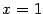
и
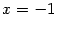
, которые обращают в 0 скобки
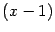
и
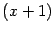
соответственно. При
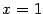
получаем:
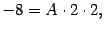
откуда
При
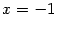
получаем:
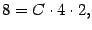
откуда
Больше "удобных" значений
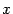
нет. Подставим
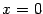
, то есть приравняем свободные члены левой и правой частей:
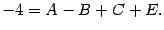
С учётом того, что
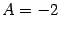
и
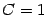
, получаем уравнение
Теперь начнём приравнивать коэффициенты при одинаковых степенях
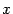
в левой и правой частях. Приравниваем коэффициенты при
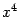
:
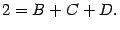
С учётом
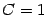
получаем второе уравнение:
Теперь приравняем коэффициенты при
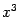
:
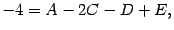
или
Получили систему из трёх линейных уравнений для трёх неизвестных
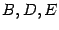
:
Решая эту систему, получаем
Подставляя найденные коэффициенты, получаем конкретный вид разложения дроби в сумму простейших:
Значит,
Заметим, что ввиду того, что подынтегральная функция имеет разрывы при
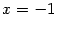
и
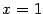
, слагаемое
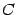
означает в данной формуле кусочно постоянную функцию, принимающую постоянные (но, может быть, различные) значения на интервалах
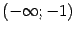
,
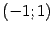
и
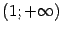
.
Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции
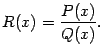
![]() , то дробь
, то дробь ![]() называется правильной, а если
называется правильной, а если ![]() , то неправильной. Если дробь неправильная, то её числитель
, то неправильной. Если дробь неправильная, то её числитель ![]() можно поделить на знаменатель
можно поделить на знаменатель ![]() , получив при этом частное
, получив при этом частное ![]() и остаток
и остаток ![]() , степень которого
, степень которого ![]() меньше
меньше ![]() . Это означает, что
. Это означает, что 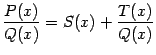
![]() , то есть многочлена
, то есть многочлена ![]() , не возникает никаких проблем, так что в дальнейшем мы можем заняться выяснением способов интегрирования лишь правильных рациональных дробей.
, не возникает никаких проблем, так что в дальнейшем мы можем заняться выяснением способов интегрирования лишь правильных рациональных дробей. ![]() и остатка
и остатка ![]() можно применять алгоритм деления многочленов "столбиком". Приведём пример.
можно применять алгоритм деления многочленов "столбиком". Приведём пример. 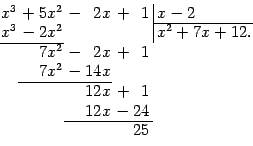
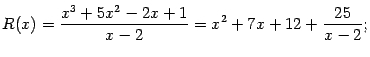
![]() раскладывается в произведение вещественных линейных и квадратичных множителей, то есть имеет вид
раскладывается в произведение вещественных линейных и квадратичных множителей, то есть имеет вид 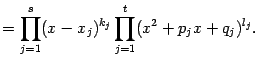
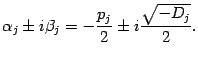
![]() можно выписать, если каким-либо способом отыскать все его корни, как вещественные, так и комплексные, и найти их кратности. Заметим также, что сумма кратностей всех корней равна степени многочлена:
можно выписать, если каким-либо способом отыскать все его корни, как вещественные, так и комплексные, и найти их кратности. Заметим также, что сумма кратностей всех корней равна степени многочлена: ![]() , то это означает, что
, то это означает, что ![]() делится на бином
делится на бином ![]() без остатка:
без остатка: 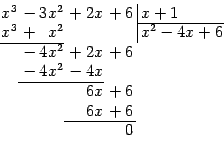
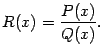
![]() -- простейшая дробь первого типа;
-- простейшая дробь первого типа; ![]() , где
, где ![]() , -- простейшая дробь второго типа;
, -- простейшая дробь второго типа; ![]() -- простейшая дробь третьего типа;
-- простейшая дробь третьего типа; ![]() , где
, где ![]() , -- простейшая дробь четвёртого типа.
, -- простейшая дробь четвёртого типа. ![]() и
и ![]() -- некоторые постоянные.
-- некоторые постоянные. ![]() раскладывается в сумму простейших дробей указанных четырёх типов.
раскладывается в сумму простейших дробей указанных четырёх типов. ![]() имеется множитель
имеется множитель ![]() , то разложение будет содержать слагаемое в виде простейшей дроби первого типа
, то разложение будет содержать слагаемое в виде простейшей дроби первого типа ![]() , где
, где ![]() -- некоторое число.
-- некоторое число. ![]() , где
, где ![]() , то разложение будет содержать серию слагаемых, в количестве
, то разложение будет содержать серию слагаемых, в количестве ![]() штук, вида
штук, вида ![]() , где
, где ![]() , -- это простейшие дроби второго и (последняя) первого типа. (Следует заметить, однако, что непременно присутствует в разложении лишь слагаемое со старшей степенью, равной
, -- это простейшие дроби второго и (последняя) первого типа. (Следует заметить, однако, что непременно присутствует в разложении лишь слагаемое со старшей степенью, равной ![]() ; может оказаться, что некоторые, или даже все, остальные слагаемые имеют числители
; может оказаться, что некоторые, или даже все, остальные слагаемые имеют числители ![]() .)
.) ![]() , то разложение будет содержать слагаемое, равное соответствующей простейшей дроби третьего типа,
, то разложение будет содержать слагаемое, равное соответствующей простейшей дроби третьего типа, ![]() , где
, где ![]() и
и ![]() -- некоторые числа.
-- некоторые числа. ![]() , где
, где ![]() , то разложение будет содержать серию слагаемых, в количестве
, то разложение будет содержать серию слагаемых, в количестве ![]() штук, вида
штук, вида ![]() , где
, где ![]() ; -- это простейшие дроби четвёртого и (последняя) третьего типа. В разложении непременно присутствует лишь слагаемое со старшей степенью, равной
; -- это простейшие дроби четвёртого и (последняя) третьего типа. В разложении непременно присутствует лишь слагаемое со старшей степенью, равной ![]() , а остальные слагаемые могут в некоторых случаях оказаться равными 0.
, а остальные слагаемые могут в некоторых случаях оказаться равными 0. ![]() в сумму простейших дробей по формуле (2.4), привести к общему знаменателю сумму, стоящую в правой части. Заметим, что этот общий знаменатель, очевидно, равен
в сумму простейших дробей по формуле (2.4), привести к общему знаменателю сумму, стоящую в правой части. Заметим, что этот общий знаменатель, очевидно, равен ![]() . Получим, что в левой и правой части равенства стоят дроби с одинаковыми знаменателями; значит, и числители у них также тождественно равны. Числитель в правой части содержит неизвестные постоянные
. Получим, что в левой и правой части равенства стоят дроби с одинаковыми знаменателями; значит, и числители у них также тождественно равны. Числитель в правой части содержит неизвестные постоянные ![]() , а числитель левой части -- нет.
, а числитель левой части -- нет. ![]() и получать значения постоянных или линейные уравнения, которым они удовлетворяют; либо приравнивать друг к другу коэффициенты при одинаковых степенях
и получать значения постоянных или линейные уравнения, которым они удовлетворяют; либо приравнивать друг к другу коэффициенты при одинаковых степенях ![]() в числителях левой и правой частей: эти коэффициенты также совпадают вследствие тождественности числителей. Это также будет давать линейные уравнения, которым должны удовлетворять неизвестные коэффициенты. Оба описанных способа получения соотношений между коэффициентами можно комбинировать друг с другом так, чтобы найти коэффициенты наиболее удобным способом.
в числителях левой и правой частей: эти коэффициенты также совпадают вследствие тождественности числителей. Это также будет давать линейные уравнения, которым должны удовлетворять неизвестные коэффициенты. Оба описанных способа получения соотношений между коэффициентами можно комбинировать друг с другом так, чтобы найти коэффициенты наиболее удобным способом. 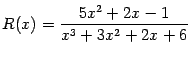
![]() , для которого в предыдущем примере мы нашли разложение на множители:
, для которого в предыдущем примере мы нашли разложение на множители: ![]() . Поэтому сумма будет состоять из двух слагаемых: простейшей дроби первого типа, соответствующей линейному множителю
. Поэтому сумма будет состоять из двух слагаемых: простейшей дроби первого типа, соответствующей линейному множителю ![]() , и простейшей дроби третьего типа, соответствующей квадратичному множителю
, и простейшей дроби третьего типа, соответствующей квадратичному множителю ![]() . Итак, вид разложения таков:
. Итак, вид разложения таков: 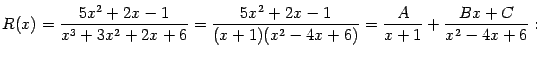
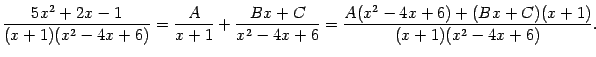
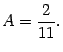
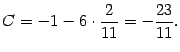
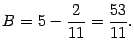
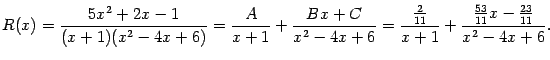
![]() в виде:
в виде: 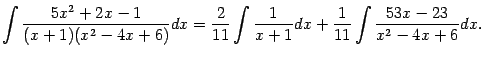
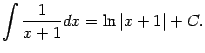
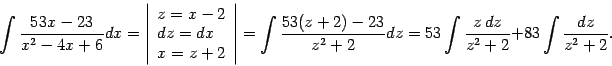
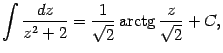
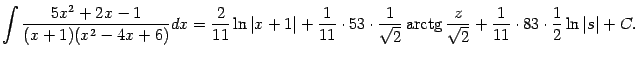
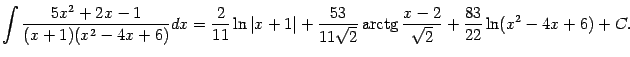
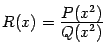 , где
, где 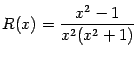
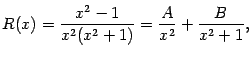
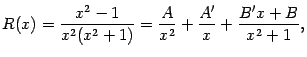
![]() -- нечётная функция от
-- нечётная функция от ![]() , в искомом разложении можно оставить одни лишь нечётные слагаемые: например, разложение дроби
, в искомом разложении можно оставить одни лишь нечётные слагаемые: например, разложение дроби 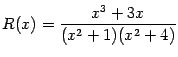
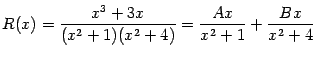
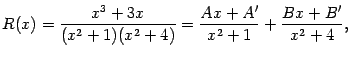
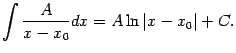
![]() :
: 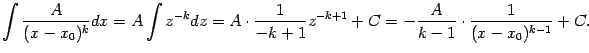
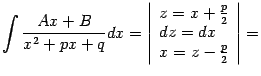
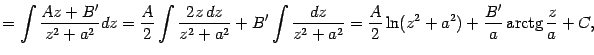
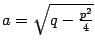 и
и 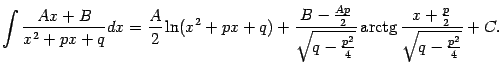
![]() , после чего интеграл
, после чего интеграл ![]() приводится к виду
приводится к виду ![]() , где
, где ![]() . Разбиваем этот интеграл на два слагаемых:
. Разбиваем этот интеграл на два слагаемых: