‹-- Назад
Использование непрерывности функций при вычислении пределов
Выше, в примерах 2.17 и 2.23, мы отмечали, что, фактически, при вычислении этих пределов использовали соображения, связанные с непрерывностью функций. Дадим теперь строгое определение непрерывности и обсудим способы вычисления пределов с помощью этого понятия.
Там же была получена формула (2.4): ![]() Пользуясь тем, что
Пользуясь тем, что ![]() , и сделав замену
, и сделав замену ![]() , получим, что
, получим, что ![]() Поэтому и
Поэтому и
Покажем, что функция ![]() непрерывна при любом
непрерывна при любом ![]() . По определению, для этого нужно доказать, что
. По определению, для этого нужно доказать, что
(здесь мы воспользовались линейностью предела;
Совершенно аналогично, с использованием формулы
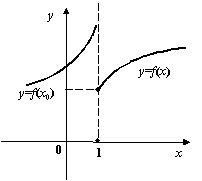
Пусть функция ![]() определена на некотором полуинтервале
определена на некотором полуинтервале ![]() (
( ![]() ), примыкающем к точке
), примыкающем к точке ![]() слева. Функция
слева. Функция ![]() называется непрерывной слева в точке
называется непрерывной слева в точке ![]() , если существует
, если существует ![]() , и
, и
Из теоремы о связи односторонних пределов с двусторонним сразу следует такая
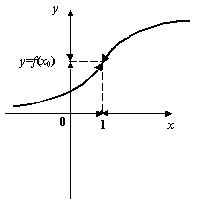
Поскольку ![]() , то непрерывность функции в точке
, то непрерывность функции в точке ![]() означает, что обозначения функции
означает, что обозначения функции ![]() и предела
и предела ![]() можно поменять местами:
можно поменять местами:
То же касается и непрерывности слева и справа.
Назовём элементарной любую функцию ![]() переменного
переменного ![]() из следующего списка:
из следующего списка:
При этом в число элементарных функций попадают, например, все многочлены
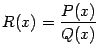
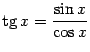 ,
, Однако не все функции, рассматривающиеся в курсе математического анализа, являются элементарными. Примером может служить довольно часто употребляющаяся функция
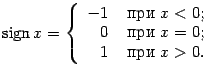
Если бы не значение ![]() , её можно было бы рассматривать как элементарную: при
, её можно было бы рассматривать как элементарную: при ![]() она совпадает с функцией
она совпадает с функцией
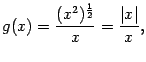
Частичное доказательство теоремы мы приведём ниже, в главе о свойствах непрерывных функций. Заметим, что выше мы уже доказали непрерывность функции ![]() . Полное доказательство теоремы можно найти в подробных учебниках по математическому анализу, например, Г. М. Фихтенгольц, Курс дифференциального и интегрального исчисления, т. 1 или С. М. Никольский, Курс математического анализа, т. 1.
. Полное доказательство теоремы можно найти в подробных учебниках по математическому анализу, например, Г. М. Фихтенгольц, Курс дифференциального и интегрального исчисления, т. 1 или С. М. Никольский, Курс математического анализа, т. 1.
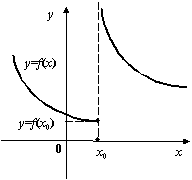
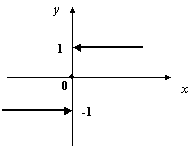
В качестве примера рассмотрим только что введённую функцию 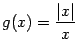 . Её график таков:
. Её график таков:

Для любой точки ![]() из области определения этой функции либо
из области определения этой функции либо ![]() , и тогда
, и тогда ![]() при всех
при всех ![]() из некоторой окрестности точки
из некоторой окрестности точки ![]() , либо
, либо ![]() , и тогда
, и тогда ![]() при всех
при всех ![]() из некоторой окрестности точки
из некоторой окрестности точки ![]() . Очевидно, что тогда в первом случае
. Очевидно, что тогда в первом случае
В случае функции ![]() всё дело "портит" точка
всё дело "портит" точка ![]() : очевидно, что
: очевидно, что
Используя непрерывность элементарных функций, на основании общих теорем можно во многих (простых) случаях находить значение пределов прямой подстановкой предельного значения ![]() в выражение, стоящее под знаком предела. Именно так мы поступим при вычислении предела в следующем примере.
в выражение, стоящее под знаком предела. Именно так мы поступим при вычислении предела в следующем примере.
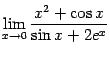 .
. Поскольку функция 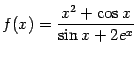 -- элементарная, причём
-- элементарная, причём ![]() -- точка её области определения (так как
-- точка её области определения (так как ![]() ), то для нахождения предела достаточно воспользоваться равенством (2.6) и подставить вместо
), то для нахождения предела достаточно воспользоваться равенством (2.6) и подставить вместо ![]() предельное значение 0:
предельное значение 0:
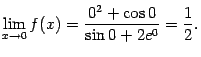
Прямую подстановку использовать нельзя в тех случаях, когда мы не можем вычислить значение элементарной функции, стоящей под знаком предела, в данной предельной точке ![]() . В этом случае говорят, что задающее функцию выражение, а также и сам предел представляют собой неопределённость. Выше мы уже встречались с неопределённостями вида
. В этом случае говорят, что задающее функцию выражение, а также и сам предел представляют собой неопределённость. Выше мы уже встречались с неопределённостями вида ![]() . Бывают ещё неопределённости вида
. Бывают ещё неопределённости вида ![]() ,
, ![]() ,
, ![]() ,
, ![]() и других видов, заданные выражениями, не имеющими формального смысла. С символами в этих выражениях нельзя обращаться, как с числами в обычных дробях, разностях, произведениях и т. д. В частности, "дроби"
и других видов, заданные выражениями, не имеющими формального смысла. С символами в этих выражениях нельзя обращаться, как с числами в обычных дробях, разностях, произведениях и т. д. В частности, "дроби" ![]() ,
, ![]() вовсе не всегда означают пределы, значение которых равно единице. Например,
вовсе не всегда означают пределы, значение которых равно единице. Например, 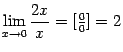 , а
, а 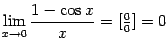 ;
; 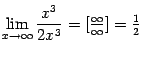 , а
, а 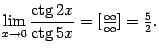 (Вычислите все эти пределы в качестве упражнения.) "Разности" вида
(Вычислите все эти пределы в качестве упражнения.) "Разности" вида ![]() отнюдь не всегда обозначают неопределённости, которые после раскрытия предела дадут 0. Например,
отнюдь не всегда обозначают неопределённости, которые после раскрытия предела дадут 0. Например, ![]() (здесь на самом деле получается 0), а
(здесь на самом деле получается 0), а ![]() . (Эти два примера будут вам предложены для решения ниже, в разделе Упражнения на вычисление пределов.)
. (Эти два примера будут вам предложены для решения ниже, в разделе Упражнения на вычисление пределов.)
Так что получается, что вся теория вычисления (нетривиальных) пределов -- это изучение способов раскрытия неопределённостей.
Во многих случаях, чтобы раскрыть неопределённость, достаточно каким-либо образом преобразовать стоящую под знаком предела функцию, после чего нахождение предела сводится к применению общих теорем (о пределе суммы, произведения, частного и т. п.), а также теорем о первом и втором замечательных пределах. Многие такие примеры мы разбирали выше. А вот ещё один типичный пример.
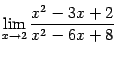 .
. Данный предел представляет собой неопределённость, так как при ![]() как числитель, так и знаменатель обращаются в 0 (это неопределённость вида
как числитель, так и знаменатель обращаются в 0 (это неопределённость вида ![]() ). Так что просто подставить 2 вместо
). Так что просто подставить 2 вместо ![]() в исходную дробь нельзя. Однако если разложить числитель и знаменатель на множители (для чего найдём корни числителя:
в исходную дробь нельзя. Однако если разложить числитель и знаменатель на множители (для чего найдём корни числителя: ![]() и
и ![]() -- и знаменателя:
-- и знаменателя: ![]() и
и ![]() ), получим
), получим ![]() и
и ![]() , и видно, что дробь (при
, и видно, что дробь (при ![]() ) можно упростить, сократив на
) можно упростить, сократив на ![]() . Поскольку при
. Поскольку при ![]() мы считаем, что
мы считаем, что ![]() , то
, то
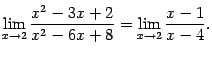
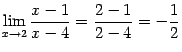 и, следовательно,
и, следовательно, 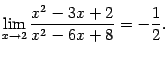
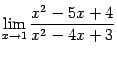 . (При этом числитель и знаменатель можно сократить на
. (При этом числитель и знаменатель можно сократить на
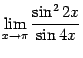 . (При этом знаменатель можно представить в виде
. (При этом знаменатель можно представить в виде