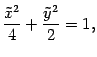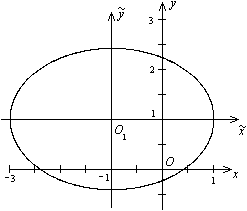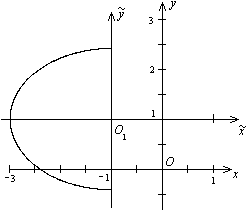‹-- Назад
Параллельный перенос системы координат
Пусть на плоскости заданы две декартовы прямоугольные системы координат:
("старая") и
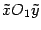
("новая"), причем как оси абсцисс, так и оси ординат обеих систем параллельны и одинаково направлены (рис. 12.19)
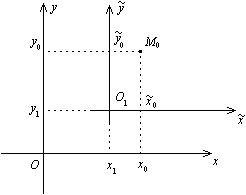
Рис.12.19.Параллельный перенос системы координат В этом случае говорят, что одна система координат получается из другой "параллельным переносом".
Пусть начало 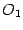 "новой" системы координат имеет в "старой" системе координат координаты
"новой" системы координат имеет в "старой" системе координат координаты 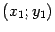 , и пусть
, и пусть 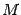 -- некоторая точка плоскости. Обозначим координаты точки
-- некоторая точка плоскости. Обозначим координаты точки 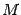 в "старой" системе координат
в "старой" системе координат 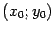 , а в "новой" --
, а в "новой" -- 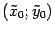 . Из рис. 12.19 ясно, что
. Из рис. 12.19 ясно, что 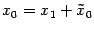 ,
, 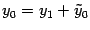 . Откуда
. Откуда 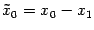 ,
, 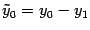 . Так как точка
. Так как точка 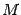 взята произвольно, то индекс 0 в записи ее координат, как "старых", так и "новых", можно убрать. Получаем связь между "старыми" и "новыми" координатами точки при параллельном переносе осей координат:
взята произвольно, то индекс 0 в записи ее координат, как "старых", так и "новых", можно убрать. Получаем связь между "старыми" и "новыми" координатами точки при параллельном переносе осей координат:
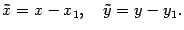 | (12.11) |
Выясним теперь, как связаны друг с другом уравнения одной и той же кривой в "старых" и "новых" координатах.
Предложение 12.6 Пусть некоторая кривая задана уравнением 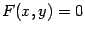 . Тогда в системе координат
. Тогда в системе координат 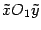 , полученной параллельным переносом, с началом в точке
, полученной параллельным переносом, с началом в точке 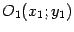 уравнение кривой будет иметь вид
уравнение кривой будет иметь вид 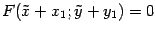 .
. Однако, для практического использования это предложение удобнее сформулировать немного подругому.
Предложение 12.7 Пусть некоторая кривая задана уравнением 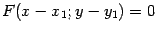 . Тогда в системе координат
. Тогда в системе координат 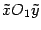 , полученной параллельным переносом, с началом в точке
, полученной параллельным переносом, с началом в точке 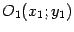 уравнение кривой будет иметь вид
уравнение кривой будет иметь вид 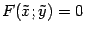 .
. Доказательство обоих предложений очевидным образом следует из формул (12.11) связи между старыми и новыми координатами.
Пример 12.7 Нарисуйте кривую
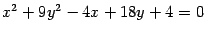
и найдите ее фокусы.
Решение. Выделим полные квадраты по переменным 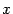 и
и 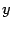 (см. пример 12.1):
(см. пример 12.1):
Откуда
Разделим обе части на 9:
Введем новую систему координат с началом в точке
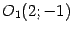
, получающуюся из старой параллельным переносом. По
предложению 12.7 получим, что кривая задается уравнением
а это -- каноническое уравнение эллипса с полуосями 3 и 1. Сделаем рисунок (рис. 12.20).
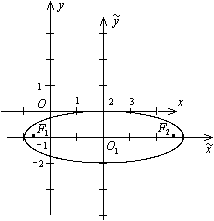
Рис.12.20.Эллипс, заданный уравнением 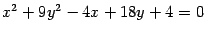
Из формулы (12.5) 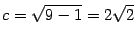 . Поэтому фокусы в новой системе координат имеют координаты
. Поэтому фокусы в новой системе координат имеют координаты 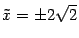 ,
, 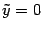 . Используя формулы (12.11), находим старые координаты фокусов
. Используя формулы (12.11), находим старые координаты фокусов 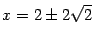 ,
, 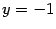 . Таким образом, фокусами являются точки
. Таким образом, фокусами являются точки 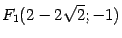 ,
, 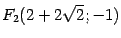 .
.
Пример 12.8 Постройте параболу
найдите ее фокус и директрису.
Решение. Преобразуем уравнение к виду 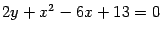 и выделим полный квадрат по переменному
и выделим полный квадрат по переменному 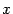 :
:
Из этого уравнения получим
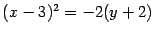
. Произведем параллельный перенос осей координат:
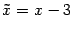
,
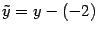
, новое начало координат --
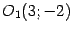
. В новых координатах уравнение параболы примет вид
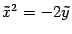
, которое тоже не является каноническим. Но если мы изменим направление оси ординат и переобозначим оси:
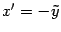
,
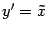
, то получим уравнение
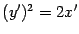
. Это уравнение -- каноническое,
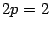
,
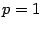
. Строим оси и параболу (рис. 12.21).
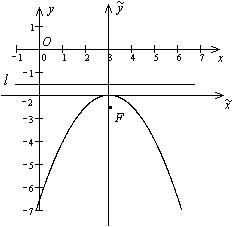
Рис.12.21.Парабола, заданная уравнением 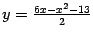
В системе координат 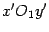 фокус имеет координаты
фокус имеет координаты 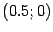 , а директриса задается уравнением
, а директриса задается уравнением 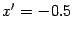 . В системе координат
. В системе координат 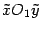 координаты фокуса --
координаты фокуса -- 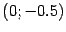 , а уравнение директрисы
, а уравнение директрисы 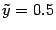 . Наконец, в исходной системе координат
. Наконец, в исходной системе координат 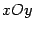 получим фокус
получим фокус 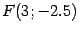 и уравнение директрисы
и уравнение директрисы 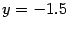 , что и служит ответом к задаче.
, что и служит ответом к задаче.
Пример 12.9 Постройте кривую
Решение. Преобразуем уравнение к виду
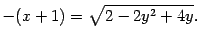 | (12.12) |
Возведем обе части в квадрат:
При этом появились новые точки, которые удовлетворяют последнему уравнению, но не удовлетворяют уравнению (
12.12). Эти посторонние точки мы отбросим потом. Выделим полный квадрат по переменному
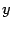
:
то есть
Обе части разделим на 4 и произведем параллельный перенос системы координат:
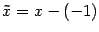
,
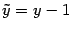
. Получим уравнение
которое является каноническим уравнением эллипса с полуосями: 2 и
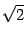
. Нарисуем его (рис. 12.22).
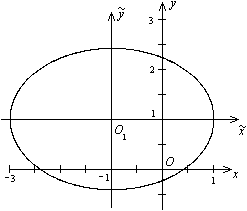
Рис.12.22.Эллипс, заданный уравнением 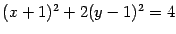
Чтобы отбросить посторонние точки, возникшие при возведении в квадрат, преобразуем уравнение (12.12) к виду
Из этого уравнения видно, что
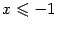
. Поэтому от нарисованного ранее эллипса нужно оставить только левую половину (рис. 12.23).
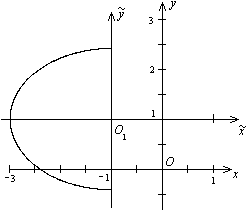
Рис.12.23.Кривая, заданная уравнением 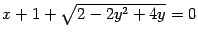
Последний рисунок и является ответом к задаче.
Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции

![]() "новой" системы координат имеет в "старой" системе координат координаты
"новой" системы координат имеет в "старой" системе координат координаты ![]() , и пусть
, и пусть ![]() -- некоторая точка плоскости. Обозначим координаты точки
-- некоторая точка плоскости. Обозначим координаты точки ![]() в "старой" системе координат
в "старой" системе координат ![]() , а в "новой" --
, а в "новой" -- ![]() . Из рис. 12.19 ясно, что
. Из рис. 12.19 ясно, что ![]() ,
, ![]() . Откуда
. Откуда ![]() ,
, ![]() . Так как точка
. Так как точка ![]() взята произвольно, то индекс 0 в записи ее координат, как "старых", так и "новых", можно убрать. Получаем связь между "старыми" и "новыми" координатами точки при параллельном переносе осей координат:
взята произвольно, то индекс 0 в записи ее координат, как "старых", так и "новых", можно убрать. Получаем связь между "старыми" и "новыми" координатами точки при параллельном переносе осей координат: ![]() и
и ![]() (см. пример 12.1):
(см. пример 12.1): 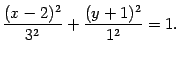
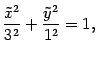
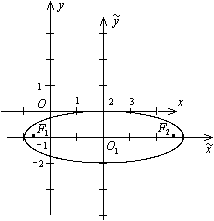
![]() . Поэтому фокусы в новой системе координат имеют координаты
. Поэтому фокусы в новой системе координат имеют координаты ![]() ,
, ![]() . Используя формулы (12.11), находим старые координаты фокусов
. Используя формулы (12.11), находим старые координаты фокусов ![]() ,
, ![]() . Таким образом, фокусами являются точки
. Таким образом, фокусами являются точки ![]() ,
, ![]() .
. 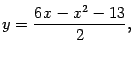
![]() и выделим полный квадрат по переменному
и выделим полный квадрат по переменному ![]() :
: 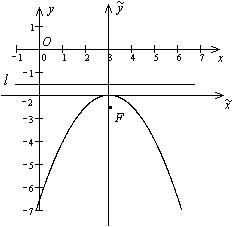
![]() фокус имеет координаты
фокус имеет координаты ![]() , а директриса задается уравнением
, а директриса задается уравнением ![]() . В системе координат
. В системе координат ![]() координаты фокуса --
координаты фокуса -- ![]() , а уравнение директрисы
, а уравнение директрисы ![]() . Наконец, в исходной системе координат
. Наконец, в исходной системе координат ![]() получим фокус
получим фокус ![]() и уравнение директрисы
и уравнение директрисы ![]() , что и служит ответом к задаче.
, что и служит ответом к задаче.