‹-- Назад

Производные некоторых элементарных функций

    

1. Выше мы уже рассмотрели линейную функцию и показали, что её производная равна угловому коэффициенту :

2. Рассмотрим функцию . Дадим аргументу приращение и найдём приращение функции: . Поэтому

(Можно доказать эту формулу и так:

Здесь мы применили формулу (4.9).) Точно так же для функции получаем: , откуда

(И здесь, применяя формулу (4.9), мы можем действовать так:

Такие же вычисления для функции при целом можно провести, разложив по формуле бинома Ньютона (см. гл. 2). При этом получится формула

(4.12)

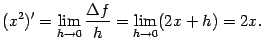
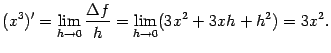
(Проведите это вычисление самостоятельно в качестве упражнения. Другой способ доказательства этой формулы -- представить в виде и применить метод математической индукции, воспользовавшись тем, что при и 3 формула уже доказана.) При и формула (4.12) совпадает, соответственно, с формулами (4.5) и (4.6). Ниже мы докажем, что эта формула верна при любом , в том числе при дробных и отрицательных значениях .

3. Найдём производную функции в точке . Преобразуем приращение функции следующим образом:

Поэтому

поскольку вследствие непрерывности элементарной функции в любой точке . Получили в итоге формулу , то есть формулу (4.12) при .

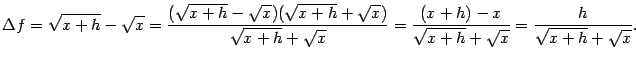
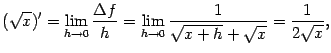
4. Пусть 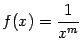, где . Производную этой функции можно подсчитать по формуле производной частного (формула (4.10)):

то есть . Эта формула совпадает с формулой (4.12) при отрицательных целых .

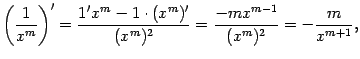
В частности, получаем при

и при

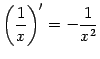
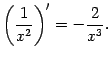
5. Пусть . Тогда приращение функции равно

а производная --

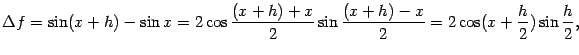
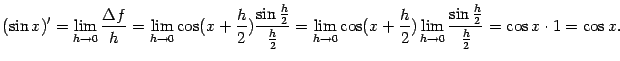
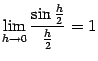При этом мы воспользовались тем, что , так как  -- непрерывная функция, и тем, что (это первый замечательный предел).

6. Пусть . Тогда приращение функции равно

а производная --

При этом мы воспользовались непрерывностью синуса, откуда и первым замечательным пределом.

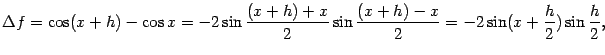
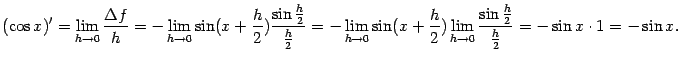
7. Рассмотрим функцию как отношение и применим для нахождения производной формулу (4.10). Получаем:

8. Аналогично, для функции получаем

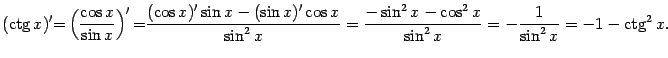
9. Пусть ( ). Тогда приращение функции равно

а разностное отношение --

Теперь вычислим производную:


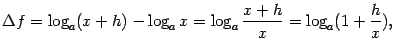
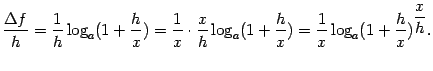
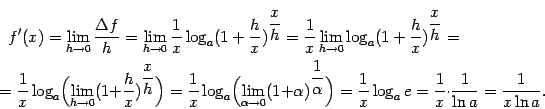
При вычислении предела мы, во-первых, воспользовались непрерывностью логарифмической функции и переставили знаки предела и логарифма; во-вторых, сделали замену , при этом при ; в-третьих, был использован второй замечательный предел: .

Из полученной формулы

при вытекает, что

        Пример 4.3   Найдём производную функции

При вычислим производную как производную произведения:

При производную вычислим по формуле, служащей определением производной:

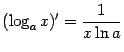
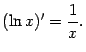
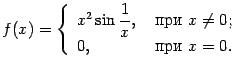
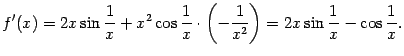
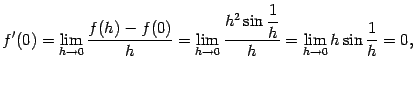
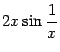поскольку получили предел произведения бесконечно малой величины и ограниченной величины . Итак, , однако это значение не является пределом при , то есть производная имеет при разрыв второго рода. Действительно, в выражении для при первое слагаемое стремится к 0 при 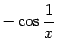, однако второе слагаемое не стремится ни к какому пределу при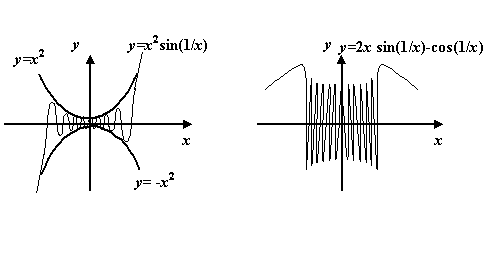 , совершая вблизи 0 бесконечно много колебаний.

Рис.4.5.Графики функции и её производной


Этот пример показывает, что производная, даже если она всюду существует, не обязана быть непрерывной функцией.     





Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции

на главную
Hosted by uCoz