‹-- Назад
Выпуклые множества и функции
Выше мы дали определение выпуклого множества: напомним, что множество ![]() -- выпуклое, если вместе с любыми двумя точками
-- выпуклое, если вместе с любыми двумя точками ![]() множеству
множеству ![]() принадлежат все точки
принадлежат все точки ![]() отрезка, соединяющего в пространстве
отрезка, соединяющего в пространстве ![]() точку
точку ![]() с точкой
с точкой ![]() . Заметим, что отрезок, состоящий из точек
. Заметим, что отрезок, состоящий из точек ![]() , можно параметризовать следующим образом:
, можно параметризовать следующим образом: ![]() Тогда при
Тогда при ![]() будет получаться точка
будет получаться точка ![]() , при
, при ![]() -- точка
-- точка ![]() , а при
, а при ![]() -- промежуточные точки отрезка, так что обозначения точек отрезка как
-- промежуточные точки отрезка, так что обозначения точек отрезка как ![]() будут согласованы с обозначениями его концов.
будут согласованы с обозначениями его концов.
На следующем рисунке изображены два множества на плоскости ![]() : одно выпуклое, а другое нет.
: одно выпуклое, а другое нет.
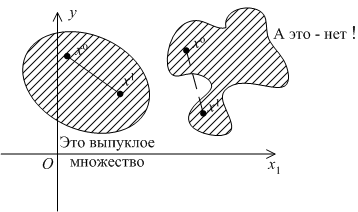
Выпуклыми в пространстве
Заметим также, что, согласно определению, выпуклы также все одноточечные множества ![]() и пустое множество
и пустое множество ![]() .
.
Доказательство. Пусть точки ![]() и
и ![]() принадлежат
принадлежат ![]() ; тогда обе они принадлежат каждому из множеств
; тогда обе они принадлежат каждому из множеств ![]() . Значит, если
. Значит, если ![]() -- произвольная точка отрезка, соединяющего
-- произвольная точка отрезка, соединяющего ![]() и
и ![]() , то она принадлежит
, то она принадлежит ![]() , поскольку
, поскольку ![]() выпукло. Но так как
выпукло. Но так как ![]() для всех
для всех ![]() , то
, то ![]() , что и требовалось доказать.
, что и требовалось доказать.
Из этой теоремы следует, например, что прямая в ![]() -мерном пространстве (её можно задать как векторным уравнением:
-мерном пространстве (её можно задать как векторным уравнением: ![]() , где
, где ![]() -- фиксированные векторы, а
-- фиксированные векторы, а ![]() -- параметр, так и в виде пересечения гиперплоскостей
-- параметр, так и в виде пересечения гиперплоскостей ![]() ) является выпуклым множеством. Действительно, каждая гиперплоскость
) является выпуклым множеством. Действительно, каждая гиперплоскость ![]() -- выпуклое множество.
-- выпуклое множество.
Проколотая окрестность любой точки ![]() , то есть множество
, то есть множество ![]() (
( ![]() ), не является выпуклым. Чтобы показать это, достаточно выбрать любой ненулевой вектор
), не является выпуклым. Чтобы показать это, достаточно выбрать любой ненулевой вектор ![]() длины меньше
длины меньше ![]() и рассмотреть точки проколотой окрестности
и рассмотреть точки проколотой окрестности ![]() и
и ![]() , расположенные симметрично относительно точки
, расположенные симметрично относительно точки ![]() . Тогда середина отрезка, соединяющего
. Тогда середина отрезка, соединяющего ![]() с
с ![]() , то есть точка
, то есть точка ![]() , совпадает с
, совпадает с ![]() и, следовательно, не лежит в проколотой окрестности точки
и, следовательно, не лежит в проколотой окрестности точки ![]() .
.
Если ![]() , то есть речь идёт о подмножествах прямой
, то есть речь идёт о подмножествах прямой ![]() , то выпуклые множества можно описать полностью: это а) пустое множество; б) все одноточечные множества; в) все интервалы вида
, то выпуклые множества можно описать полностью: это а) пустое множество; б) все одноточечные множества; в) все интервалы вида ![]() (где
(где ![]() может равняться
может равняться ![]() , а
, а ![]() может равняться
может равняться ![]() ); г) все полуинтервалы вида
); г) все полуинтервалы вида ![]() (где
(где ![]() может равняться
может равняться ![]() ) и
) и ![]() (где
(где ![]() может равняться
может равняться ![]() ); наконец, д) все отрезки вида
); наконец, д) все отрезки вида ![]() . Никаких других выпуклых множеств на прямой нет.
. Никаких других выпуклых множеств на прямой нет.
Напомним изученное в первом семестре определение выпуклой функции одного вещественного переменного.
и вогнутой (или выпуклой кверху), если выполняется неравенство
(То есть функция
В левой части этого неравенства стоит значение функции ![]() в производной точке
в производной точке
Если
Дадим теперь определение выпуклой функции многих переменных.
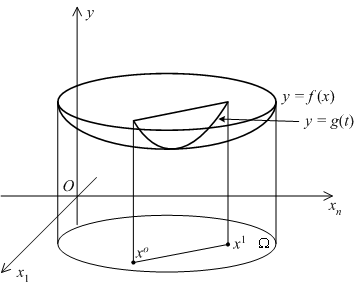
Функция
Таким образом, функция ![]() вогнута в том и только том случае, когда функция
вогнута в том и только том случае, когда функция ![]() выпукла.
выпукла.
Выпуклость функции ![]() в
в ![]() означает, что для любого отрезка
означает, что для любого отрезка ![]() с концами
с концами ![]() и
и ![]() параметризация этого отрезка в виде
параметризация этого отрезка в виде ![]() задаёт композицию
задаёт композицию ![]() , являющуюся выпуклой функцией параметра
, являющуюся выпуклой функцией параметра ![]() . Ввиду выпуклости области
. Ввиду выпуклости области ![]() , любые точки
, любые точки ![]() и
и ![]() отрезка
отрезка ![]() лежат в
лежат в ![]() , и их снова можно взять в качестве концов отрезка. Поэтому для выпуклости функции
, и их снова можно взять в качестве концов отрезка. Поэтому для выпуклости функции ![]() в области
в области ![]() необходимо и достаточно, чтобы неравенство
необходимо и достаточно, чтобы неравенство
Если при этом при всех ![]() и
и ![]() выполняется строгое неравенство
выполняется строгое неравенство
Наконец, функция ![]() называется строго вогнутой, если функция
называется строго вогнутой, если функция ![]() строго выпукла; это означает выполнение строгого неравенства
строго выпукла; это означает выполнение строгого неравенства
Геометрически (в случае ![]() ) строгая выпуклость означает, что для любой хорды графика
) строгая выпуклость означает, что для любой хорды графика ![]() точки дуги графика с теми же концами, что у хорды, лежащие в вертикальном сечении, проходящем через эту хорду, располагаются ниже точек хорды. Строгая вогутость означает, что в любом вертикальном сечении график проходит выше любого отрезка, соединяющего две точки графика.
точки дуги графика с теми же концами, что у хорды, лежащие в вертикальном сечении, проходящем через эту хорду, располагаются ниже точек хорды. Строгая вогутость означает, что в любом вертикальном сечении график проходит выше любого отрезка, соединяющего две точки графика.
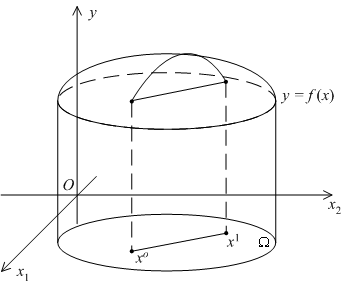
Заметим, что понятия выпуклой и вогнутой функций (а также строго выпуклой и строго вогнутой функций) в области
Дадим теперь такое алгебраическое определение.
Заметим, что выражение ![]() можно записать в виде
можно записать в виде ![]() , где
, где ![]() -- это матрица-строка, равная транспонированному столбцу
-- это матрица-строка, равная транспонированному столбцу ![]() . Вообще, верхний левый индекс
. Вообще, верхний левый индекс ![]() мы будем применять для обозначения транспонированной матрицы.
мы будем применять для обозначения транспонированной матрицы.
У симметричной матрицы равны друг другу элементы, расположенные симметрично друг другу относительно главной диагонали матрицы.
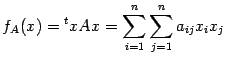
Если же симметричная матрица ![]() -- положительно определённая, то заданная ею квадратичная форма
-- положительно определённая, то заданная ею квадратичная форма ![]() является строго выпуклой.
является строго выпуклой.
Доказательство. Пусть ![]() и
и ![]() -- две произвольные точки
-- две произвольные точки ![]() и
и ![]() , где
, где ![]() , -- точка отрезка, соединяющего
, -- точка отрезка, соединяющего ![]() с
с ![]() .
.
Предположим, что матрица ![]() неотрицательно определена. Элементарные преобразования позволяют записать
неотрицательно определена. Элементарные преобразования позволяют записать ![]() в виде
в виде
Поскольку матрица
Доказательство строгой выпуклости в случае положительно определённой матрицы проводится с помощью очевидных изменений приведённого доказательства.
Другой пример выпуклой функции даёт линейная функция:
Поскольку функция ![]() , очевидно, также линейна, линейная функция
, очевидно, также линейна, линейная функция ![]() является одновременно и вогнутой (но не строго вогнутой).
является одновременно и вогнутой (но не строго вогнутой).
Если о некоторых функциях известно, что они выпуклы в области ![]() , то из них можно сконструировать другие выпуклые функции, используя следующие свойства выпуклых функций.
, то из них можно сконструировать другие выпуклые функции, используя следующие свойства выпуклых функций.
Доказательство. Пусть ![]() и
и ![]() , где
, где ![]() . Тогда
. Тогда
что и означает выпуклость функции
Поскольку, как мы доказали выше, квадратичная функция ![]() с неотрицательно определённой матрицей
с неотрицательно определённой матрицей ![]() и линейная функция
и линейная функция ![]() выпуклы, то и их сумма, согласно доказанному свойству, -- выпуклая функция. В качестве упражнения докажите, однако, ещё одно утверждение, не вытекающее из теоремы 7.17:
выпуклы, то и их сумма, согласно доказанному свойству, -- выпуклая функция. В качестве упражнения докажите, однако, ещё одно утверждение, не вытекающее из теоремы 7.17:
Указание: по сути дела, нужно повторить доказательство теоремы 7.16, с очевидными изменениями.
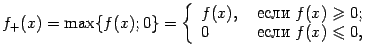
Доказательство. Пусть снова ![]() и
и ![]() , где
, где ![]() . Тогда
. Тогда
| (7.11*) | |
| (7.12) |
что и означает выпуклость функции
Доказательство. Пусть снова ![]() и
и ![]() , где
, где ![]() . Тогда, ввиду того что
. Тогда, ввиду того что ![]() , получаем:
, получаем:
Последнее неравенство следует из того, что
Следующие три утверждения остаются читателю для самостоятельного доказательства в качестве упражнения.
Если функции ![]() и
и ![]() выпуклы в области
выпуклы в области ![]() , то функция
, то функция ![]() также выпукла в
также выпукла в ![]() .
.
Если функция ![]() выпукла в области
выпукла в области ![]() , а функция одного переменного
, а функция одного переменного ![]() выпукла на интервале
выпукла на интервале ![]() , содержащем множество значений функции
, содержащем множество значений функции ![]() при всех
при всех ![]() , и
, и ![]() возрастает всюду на интервале
возрастает всюду на интервале ![]() или убывает всюду на
или убывает всюду на ![]() , то композиция
, то композиция ![]() выпукла в
выпукла в ![]() . (Например, если функция
. (Например, если функция ![]() выпукла в
выпукла в ![]() , то функция
, то функция ![]() также будет выпуклой в
также будет выпуклой в ![]() .)
.)
Выпуклые функции интересны такой своей особенностью: они не могут иметь нескольких локальных минимумов с разными значениями.
Сначала дадим такое определение.
Точка ![]() называется точкой локального минимума функции
называется точкой локального минимума функции ![]() , если существует такая окрестность
, если существует такая окрестность ![]() ,
, ![]() , что
, что ![]() при всех
при всех ![]() . Если при этом
. Если при этом ![]() при всех
при всех ![]() , не совпадающих с
, не совпадающих с ![]() , то точка
, то точка ![]() называется точкой строгого локального минимума. И в том и в другом случае значение
называется точкой строгого локального минимума. И в том и в другом случае значение ![]() называется локальным минимумом функции
называется локальным минимумом функции ![]() .
.
Точка ![]() называется точкой локального максимума функции
называется точкой локального максимума функции ![]() , если существует такая окрестность
, если существует такая окрестность ![]() ,
, ![]() , что
, что ![]() при всех
при всех ![]() . Если при этом
. Если при этом ![]() при всех
при всех ![]() , не совпадающих с
, не совпадающих с ![]() , то точка
, то точка ![]() называется точкой строгого локального максимума. И в том и в другом случае значение
называется точкой строгого локального максимума. И в том и в другом случае значение ![]() называется локальным максимумом функции
называется локальным максимумом функции ![]() .
.
любая точка локального максимума функции
Доказательство. Очевидно, что достаточно доказать лишь первое утверждение: второе следует из него сменой знака функции.
Пусть ![]() -- точка локального минимума, а в некоторой другой точке
-- точка локального минимума, а в некоторой другой точке ![]() функция имеет меньшее значение:
функция имеет меньшее значение: ![]() . Тогда в точках отрезка, соединяющего
. Тогда в точках отрезка, соединяющего ![]() с
с ![]() , то есть точках
, то есть точках ![]() , при всех
, при всех ![]() значения функции будут меньше, чем в точке
значения функции будут меньше, чем в точке ![]() :
:
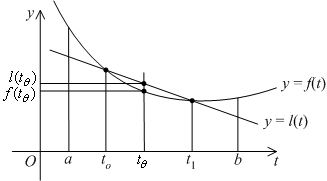
Практическая ценность этого утверждения в том, что при поиске наименьшего значения выпуклой функции в области ![]() достаточно найти любую точку локального минимума; во всех остальных точках локального минимуцма (если они существуют) значение функции будет точно такое же. Для невыпуклых функций это, конечно, не так, как видно на следующем рисунке:
достаточно найти любую точку локального минимума; во всех остальных точках локального минимуцма (если они существуют) значение функции будет точно такое же. Для невыпуклых функций это, конечно, не так, как видно на следующем рисунке:
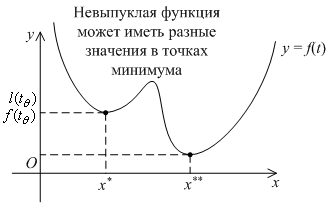
Имеет место также следующая
Доказательство. Пусть в двух разных точках ![]() и
и ![]() функция
функция ![]() принимает одно и то же значение
принимает одно и то же значение ![]() Поскольку функция строго выпукла, то в точках
Поскольку функция строго выпукла, то в точках ![]() , не совпадающих с
, не совпадающих с ![]() и с
и с ![]() , должно выполняться неравенство
, должно выполняться неравенство