‹-- Назад
Выпуклость функции
Пусть ![]() . Тогда любую точку отрезка
. Тогда любую точку отрезка ![]() можно задать как
можно задать как ![]() ,
, ![]() , а любую точку хорды -- как
, а любую точку хорды -- как ![]() . Выражение
. Выражение ![]() задаёт линейную функцию переменного
задаёт линейную функцию переменного ![]() , график которой на отрезке
, график которой на отрезке ![]() совпадает с хордой.
совпадает с хордой.
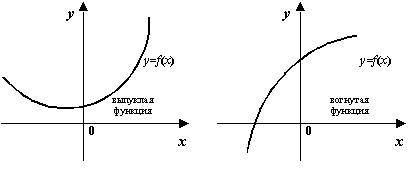
То, что график функции идёт не выше хорды, означает, что
при всех
Аналогично определяется выпуклость вверх: функция ![]() называется выпуклой вверх (или вогнутой) на интервале
называется выпуклой вверх (или вогнутой) на интервале ![]() , если график функции
, если график функции ![]() идёт не ниже хорды, соединяющей любые две точки графика
идёт не ниже хорды, соединяющей любые две точки графика ![]() и
и ![]() при
при ![]() . Это означает, что
. Это означает, что
при всех
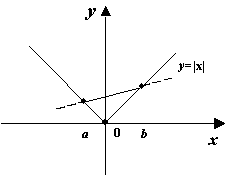
Легко видеть, что функция ![]() вогнута на интервале
вогнута на интервале ![]() в том и только том случае, когда функция
в том и только том случае, когда функция ![]() выпукла на
выпукла на ![]() .
.
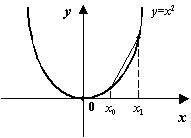
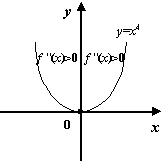
Мы привыкли изображать параболу именно так, что очевидно: хорда идёт выше графика на любом интервале ![]() . Подтвердим теперь это свойство формальной выкладкой. Имеем:
. Подтвердим теперь это свойство формальной выкладкой. Имеем:
Здесь мы использовали известное неравенство:
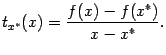
Тогда функция ![]() выпукла на интервале
выпукла на интервале ![]() в том и только том случае, когда функция
в том и только том случае, когда функция ![]() не убывает на множестве
не убывает на множестве ![]() .
.
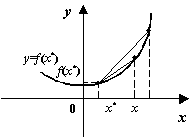
Заметим также, что функция ![]() имеет следующее свойство:
имеет следующее свойство:
Действительно,
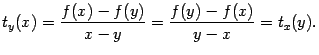 |
Доказательство теоремы 7.9. Выберем любые две точки ![]() . Предположим, что
. Предположим, что ![]() (случаи иного расположения точек
(случаи иного расположения точек ![]() рассматриваются аналогично). Поскольку
рассматриваются аналогично). Поскольку ![]() , то
, то ![]() при некотором
при некотором ![]() . Нетрудно видеть, что тогда
. Нетрудно видеть, что тогда 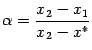 и
и 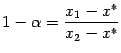 . Поэтому из выпуклости функции
. Поэтому из выпуклости функции ![]() следует, что
следует, что
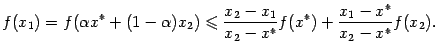
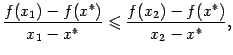
Доказательство того, что из неубывания функции ![]() следует выпуклость функции
следует выпуклость функции ![]() , можно провести, если проделать все преобразования в обратном порядке.
, можно провести, если проделать все преобразования в обратном порядке.
функция ![]() вогнута на интервале
вогнута на интервале ![]() тогда и только тогда, когда при любом
тогда и только тогда, когда при любом ![]() функция
функция ![]() не возрастает на множестве
не возрастает на множестве ![]() .
.
Доказанная теорема содержит хотя и важный, но всё же вспомогательный результат. На её основании мы получим следующее утверждение, которое уже гораздо удобнее применять на практике для исследования выпуклости.
Доказательство. Пусть ![]() -- выпуклая функция. Возьмём точки
-- выпуклая функция. Возьмём точки ![]() на интервале
на интервале ![]() так, чтобы они следовали в таком порядке:
так, чтобы они следовали в таком порядке: ![]() . По предыдущей теореме, функции
. По предыдущей теореме, функции ![]() и
и ![]() не убывают. Пользуясь также свойством (7.6), получаем цепочку:
не убывают. Пользуясь также свойством (7.6), получаем цепочку:
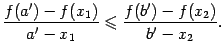
Пусть теперь производная ![]() -- неубывающая функция. Фиксируем точку
-- неубывающая функция. Фиксируем точку ![]() и найдём производную функции
и найдём производную функции 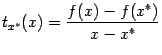 при
при ![]() . Она равна
. Она равна
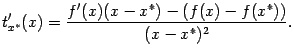
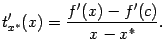
дифференцируемая функция ![]() вогнута на интервале
вогнута на интервале ![]() тогда и только тогда, когда её производная
тогда и только тогда, когда её производная ![]() не возрастает.
не возрастает.
Если функция имеет во всех точках интервала вторую производную ![]() , то для исследования выпуклости можно воспользоваться следующим утверждением, которое вытекает из доказанной теоремы.
, то для исследования выпуклости можно воспользоваться следующим утверждением, которое вытекает из доказанной теоремы.
Доказательство. Производная ![]() не убывает на
не убывает на ![]() в том и только том случае, когда
в том и только том случае, когда ![]() при всех
при всех ![]() , и не возрастает в на
, и не возрастает в на ![]() в том и только том случае, когда
в том и только том случае, когда ![]() при всех
при всех ![]() . Поэтому утверждение теоремы сразу следует из теоремы 7.10 и замечания 7.9.
. Поэтому утверждение теоремы сразу следует из теоремы 7.10 и замечания 7.9.
Именно эту теорему чаще всего применяют для исследования выпуклости и вогнутости функции на заданном интервале, а также для нахождения интервалов выпуклости и интервалов вогнутости данной функции.
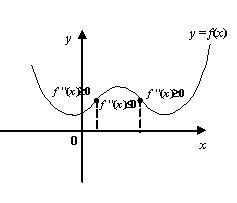
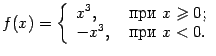
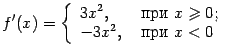
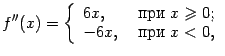
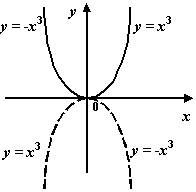
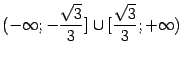 . Значит, на интервалах
. Значит, на интервалах 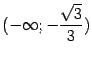 и
и 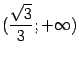 функция
функция Для нахождения интервала вогнутости нужно решить неравенство ![]() , то есть
, то есть ![]() . Решением является отрезок
. Решением является отрезок 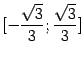 . Значит, на интервале
. Значит, на интервале 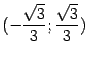 функция
функция ![]() вогнута.
вогнута.
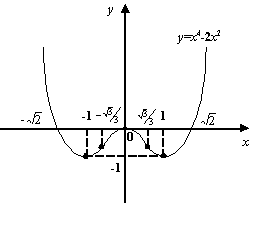
Выпуклые функции обладают следующим весьма важным свойством: они могут иметь не более одного локального минимума на интервале выпуклости. А именно, верна следующая теорема.
Доказательство теоремы. Пусть ![]() и
и ![]() -- две различные точки локального минимума функции
-- две различные точки локального минимума функции ![]() , причём
, причём ![]() и
и ![]() (случай
(случай ![]() разбирается аналогично). Положим
разбирается аналогично). Положим ![]() и рассмотрим линейную функцию
и рассмотрим линейную функцию ![]() , на графике которой лежит хорда, соединяющая точки
, на графике которой лежит хорда, соединяющая точки ![]() и
и ![]() . Так как функция
. Так как функция ![]() выпукла, то
выпукла, то ![]() при всех
при всех ![]() , то есть при всех
, то есть при всех ![]() . Это неравенство верно, в том числе, и при любом
. Это неравенство верно, в том числе, и при любом ![]() из некоторой правой окрестности точки
из некоторой правой окрестности точки ![]() , то есть при
, то есть при ![]() ,
, ![]() . Тем самым получаем для таких
. Тем самым получаем для таких ![]() :
:
Значит, предположение о том, что ![]() , не может быть верным. Точно так же доказывается, что неверно и предположение о том, что
, не может быть верным. Точно так же доказывается, что неверно и предположение о том, что ![]() . Следовательно,
. Следовательно, ![]() , то есть во всех точках локального экстремума (если их не одна) функция
, то есть во всех точках локального экстремума (если их не одна) функция ![]() принимает одно и то же значение.
принимает одно и то же значение.
Тем самым, если о функции ![]() известно, что она выпукла, и мы нашли некоторую точку локального минимума
известно, что она выпукла, и мы нашли некоторую точку локального минимума ![]() , то значение в этой точке -- это минимальное значение функции на всём рассматриваемом интервале:
, то значение в этой точке -- это минимальное значение функции на всём рассматриваемом интервале: ![]() . Если нас интересует лишь это минимальное значение, а не полный набор точек минимума, то мы можем других точек локального минимума не искать.
. Если нас интересует лишь это минимальное значение, а не полный набор точек минимума, то мы можем других точек локального минимума не искать.
если ![]() -- вогнутая функция на интервале
-- вогнутая функция на интервале ![]() и
и ![]() -- точки локального максимума, то
-- точки локального максимума, то
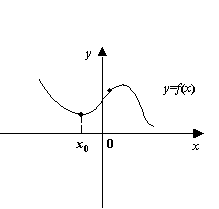
Аналогично, график гладкой функции имеет выпуклость вверх в окрестности точки локального максимума. Поэтому неравенство ![]() даёт достаточное условие локального максимума.
даёт достаточное условие локального максимума.
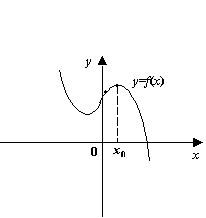
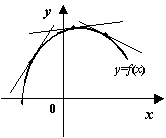
Изучим теперь связь выпуклости и вогнутости функции ![]() с взаимным расположением графика функции и касательных, проведённых к этому графику.
с взаимным расположением графика функции и касательных, проведённых к этому графику.
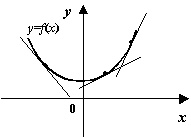
Доказательство. Применяя формулу конечных приращений, получаем:
дифференцируемая функция вогнута на интервале ![]() тогда и только тогда, когда её график идёт не выше любой касательной:
тогда и только тогда, когда её график идёт не выше любой касательной: ![]()
![]() .
.
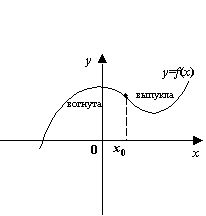
В случае, если вторая производная ![]() непрерывна, в точке перегиба
непрерывна, в точке перегиба ![]() непременно должно выполняться равенство
непременно должно выполняться равенство ![]() , поскольку, согласно теореме 7.11,
, поскольку, согласно теореме 7.11, ![]() должна менять знак при переходе через точку
должна менять знак при переходе через точку ![]() . Верно даже несколько более сильное утверждение:
. Верно даже несколько более сильное утверждение:
Доказательство. Из существования ![]() следует, что
следует, что ![]() существует при
существует при ![]() из некоторого интервала
из некоторого интервала ![]() , окружающего точку
, окружающего точку ![]() . По предположению, при достаточно малом
. По предположению, при достаточно малом ![]() , на интервалах
, на интервалах ![]() и
и ![]() направление выпуклости функции разное; пусть для определённости
направление выпуклости функции разное; пусть для определённости ![]() выпукла на
выпукла на ![]() и вогнута на
и вогнута на ![]() . Тогда функция
. Тогда функция ![]() не убывает на
не убывает на ![]() и не возрастает на
и не возрастает на ![]() , согласно теореме 7.10 и замечанию 7.9. Значит,
, согласно теореме 7.10 и замечанию 7.9. Значит, 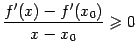 при
при ![]() и
и 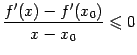 при
при ![]() . Переходя в этих двух неравенствах к пределу при базе
. Переходя в этих двух неравенствах к пределу при базе ![]() и
и ![]() соответственно и замечая, что оба предела равны
соответственно и замечая, что оба предела равны ![]() , получаем, что одновременно
, получаем, что одновременно ![]() и
и ![]() . Значит,
. Значит, ![]() , что и требовалось доказать.
, что и требовалось доказать.
Заметим однако, что не любая точка ![]() , такая что
, такая что ![]() , обязана быть точкой перегиба: при переходе через такую точку функция
, обязана быть точкой перегиба: при переходе через такую точку функция ![]() может и не сменить знак, тогда перегиба в точке
может и не сменить знак, тогда перегиба в точке ![]() нет.
нет.
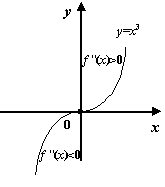
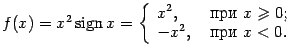 Тогда
Тогда 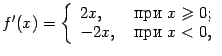 и
и 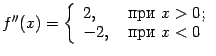 (при
(при 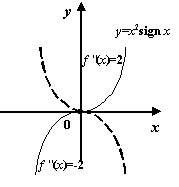
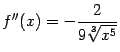 (проверьте, что это так!). При
(проверьте, что это так!). При 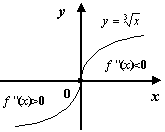
Проверьте, что любая точка ![]() (в том числе
(в том числе ![]() ) есть точка перегиба функции
) есть точка перегиба функции ![]() .
.
Итак, точки перегиба содержатся в списке тех точек ![]() , в которых либо
, в которых либо ![]() , либо
, либо ![]() не существует. Однако такая точка
не существует. Однако такая точка ![]() может и не оказаться точкой перегиба; для выяснения нужно исследовать поведение функции слева и справа от "подозрительной" точки
может и не оказаться точкой перегиба; для выяснения нужно исследовать поведение функции слева и справа от "подозрительной" точки ![]() .
.