‹-- Назад

Формула Тейлора для функции нескольких переменных

Напомним, что в случае функции одного переменного $ x$ формула Тейлора имеет вид

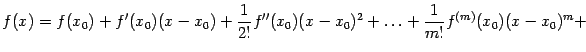$\displaystyle f(x)=f(x_0)+f'(x_0)(x-x_0)+\frac{1}{2!}f''(x_0)(x-x_0)^2+\ldots+ \frac{1}{m!}f^{(m)}(x_0)(x-x_0)^m+$    
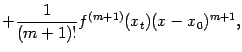$\displaystyle +\frac{1}{(m+1)!}f^{(m+1)}(x_t)(x-x_0)^{m+1},$    

где $ x_0$  -- фиксированная точка, в которой ведётся разложение, $ x$  -- текущая точка, а $ x_t$  -- некоторая точка отрезка между точками $ x_0$ и $ x$ . При этом предполагается, что функция $ f$ имеет производную $ (m+1)$ -го порядка, определённую в некторой окрестности точки $ x_0$ .

Последнее слагаемое формулы, то есть $ \frac{1}{(m+1)!}f^{(m+1)}(x_t)(x-x_0)^{m+1},$ называется остаточным членом формулы Тейлора, а многочлен от $ x$ , равный

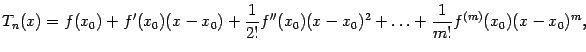
$\displaystyle T_n(x)=f(x_0)+f'(x_0)(x-x_0)+\frac{1}{2!}f''(x_0)(x-x_0)^2+\ldots+ \frac{1}{m!}f^{(m)}(x_0)(x-x_0)^m,$

называется многочленом Тейлора функции $ f$ в точке $ x_0$ .

Наша цель -- получить формулу для функции $ f$ , зависящей от $ n$ переменных $ x_1,\ \dots,\ x_n$ , частным случаем которой при $ n=1$ будет выписанная выше формула Тейлора для функции одного переменного.






Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции

на главную
Hosted by uCoz