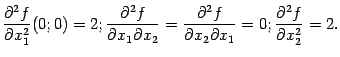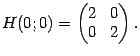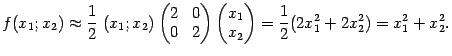‹-- Назад Двойная сумма в формуле (
9.8) содержит в качестве коэффициентов значения всех частных производных второго порядка, вычисленные в точке
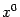
. Эти
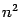
значений
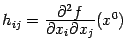
можно объединить в квадратную матрицу
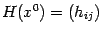
размера
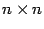
. Эта матрица
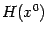
называется
матрицей Гессе функции

в точке
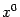
.
Если все смешанные частные производные второго порядка непрерывны, то
так что матрица Гессе в этом случае симметрична:
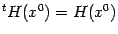
(знак
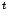
означает транспонирование матрицы).
Заметим, что линейную часть правой части формулы (9.8) можно представить в виде
(точка означает скалярное произведение), а квадратичную часть, заданную двойной суммой в формуле (
9.8), -- в виде
при этом мы считаем вектор
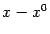
записанным в виде матрицы-столбца, а транспонированный вектор
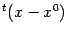
-- в виде матрицы-строки. Тем самым, получаем формулу квадратичного приближения в виде
где
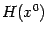
-- матрица Гессе.
В случае, когда 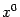 -- стационарная точка функции
-- стационарная точка функции  , градиент обращается в 0 в точке
, градиент обращается в 0 в точке 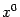 , так что получаем
, так что получаем
где
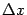
-- приращение аргумента

в точке
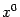
. Таким образом, в окрестности стационарной точки приращение функции ведёт себя как квадратичная функция приращения аргумента:
Пример 9.1 Рассмотрим функцию
Покажем, что начало координат
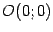
-- это стационарная точка функции
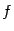
, и найдём квадратичное приближение функции
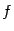
в окрестности начала координат.
Частные производные первого порядка равны
При
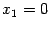
и
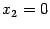
обе частные производные, действительно, обращаются в 0, так что точка
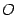
-- стационарная. Вычислим элементы матрицы Гессе
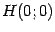
функции
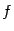
в точке
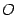
:
При 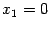 и
и 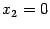 получаем:
получаем:
Значит,
Так как значение
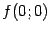
равно 0, то квадратичное приближение функции

в окрестности начала координат выглядит так:
Таким образом, при небольших
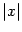
функция приближённо равна
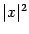
.
Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции
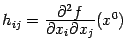 можно объединить в квадратную матрицу
можно объединить в квадратную матрицу 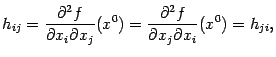
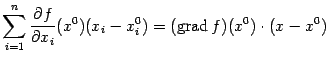
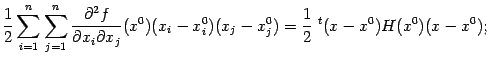
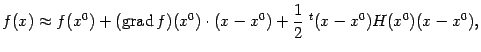
![]() -- стационарная точка функции
-- стационарная точка функции ![]() , градиент обращается в 0 в точке
, градиент обращается в 0 в точке ![]() , так что получаем
, так что получаем 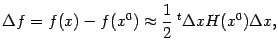
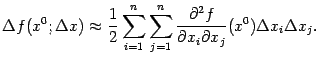
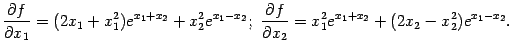
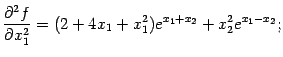
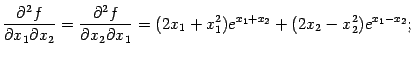
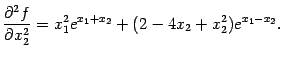
![]() и
и ![]() получаем:
получаем: