‹-- Назад
Рациональные функции и их интегрирование
Функция
называется рациональной функцией, или рациональной дробью, если она представляет собой отношение двух многочленов 
и 
:
равна 
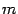
, а степень равна 
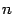
, то есть
и 
. Разделив числитель и знаменатель на число 
, мы получим, что коэффициент при старшей степени 
в знаменателе равен 1. Для дальнейшего нам будет удобно предполагать, что эта операция уже произведена, то есть что 
. Далее мы будем предполагать, что все коэффициенты 
и 
-- вещественные числа. Если 
, то дробь называется правильной, а если 
, то неправильной. Если дробь неправильная, то её числитель можно поделить на знаменатель , получив при этом частное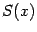 
и остаток 
, степень которого 
меньше 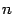. Это означает, что
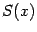
-- некоторый многочлен, называемый целой частью рациональной дроби 
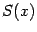
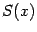. Если остаток тождественно равен 0, то многочлен делится на без остатка, и функция является многочленом, то есть совпадает со своей целой частью . С интегрированием целой части дроби , то есть многочлена , не возникает никаких проблем, так что в дальнейшем мы можем заняться выяснением способов интегрирования лишь правильных рациональных дробей.
Для нахождения частного 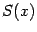и остатка можно применять алгоритм деления многочленов "столбиком". Приведём пример.
-- многочлен третьей степени -- на бином 
-- многочлен первой степени:
в виде
и остаток 
-- многочлен нулевой степени, то есть постоянную. Знаменатель 
раскладывается в произведение вещественных линейных и квадратичных множителей, то есть имеет вид
 | |
 |
Линейный множитель
повторяется в разложении 
раз, это означает, что вещественное число 
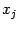
-- корень многочлена кратности . Относительно квадратичных множителей 
мы будем предполагать, что они не имеют вещественных корней, то есть что их дискриминанты отрицательны:
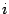
-- мнимая единица, так что 
.) Квадратичный множитель повторяется в разложении 
раз; это соответствует тому, что каждое из комплексно сопряжённых чисел 
и 
служит -кратным корнем многочлена . Указанное разложение многочлена можно выписать, если каким-либо способом отыскать все его корни, как вещественные, так и комплексные, и найти их кратности. Заметим также, что сумма кратностей всех корней равна степени многочлена:
Если найден какой-либо корень 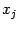, то это означает, что делится на бином без остатка:
равна 
. Точно так же, если найден какой-либо комплексный корень (тогда и сопряжённое число тоже является корнем ), то делится без остатка на произведение 
, то есть
равна 
.
-- многочлен с целочисленными коэффициентами 
, то, согласно теореме Виета, все целые корни этого многочлена содержатся среди делителей (как положительных, так и отрицательных) свободного члена 
. Проверив все эти делители, мы можем натолкнуться на некоторые из корней; если же ни один из делителей не является корнем , то это означает, что не имеет ни одного целого корня.
. Проверим, нет ли у него целых корней. Если есть, то этот корень должен быть одним из делителей свободного члена, то есть числа 6. Эти делители равны 
. Подставляем эти числа в по порядку:
. Значит, делится без остатка на бином 
. Выполним это деление "столбиком":
, найдём обычным способом:
на вещественные линейные и квадратичные множители уже получено: это 
. Кратности как корня , так и пары корней 
, оказались равными 1. Итак, предположим, что нам дана правильная рациональная дробь
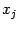
после разложения на множители может содержать множители следующих четырёх видов: (если кратность корня равна 1); 
, где 
(эти множители соответствуют вещественным корням кратности больше 1); (если кратность комплексных корней равна 1) и, наконец, 
(если кратность комплексных корней больше 1). Каждому из указанных типов множителей знаменателя соответствуют простейшие рациональные дроби, а именно:
-- простейшая дробь первого типа;
, где 
, -- простейшая дробь второго типа;
-- простейшая дробь третьего типа;
, где 
, -- простейшая дробь четвёртого типа.
Здесь 
и 
-- некоторые постоянные.
Любая правильная дробь раскладывается в сумму простейших дробей указанных четырёх типов.
Если в знаменателе дроби имеется множитель , то разложение будет содержать слагаемое в виде простейшей дроби первого типа , где -- некоторое число.
Если имеется множитель , где , то разложение будет содержать серию слагаемых, в количестве штук, вида 
, где 
, -- это простейшие дроби второго и (последняя) первого типа. (Следует заметить, однако, что непременно присутствует в разложении лишь слагаемое со старшей степенью, равной ; может оказаться, что некоторые, или даже все, остальные слагаемые имеют числители 
.)
Если в знаменателе имеется множитель 
, то разложение будет содержать слагаемое, равное соответствующей простейшей дроби третьего типа, , где и -- некоторые числа.
Наконец, если имеется множитель , где 
, то разложение будет содержать серию слагаемых, в количестве штук, вида 
, где 
; -- это простейшие дроби четвёртого и (последняя) третьего типа. В разложении непременно присутствует лишь слагаемое со старшей степенью, равной , а остальные слагаемые могут в некоторых случаях оказаться равными 0.
Сказанное можно выразить формулой, дающей разложение правильной дроби в сумму простейших дробей:
где
-- некоторые постоянные. Эти постоянные отыскивают методом неопределённых коэффициентов, выписав разложение (2.4) в соответствии с видом разложения на множители знаменателя дроби . Для отыскания неизвестных постоянных методом неопределённых коэффициентов нужно, выписав разложение в сумму простейших дробей по формуле (2.4), привести к общему знаменателю сумму, стоящую в правой части. Заметим, что этот общий знаменатель, очевидно, равен . Получим, что в левой и правой части равенства стоят дроби с одинаковыми знаменателями; значит, и числители у них также тождественно равны. Числитель в правой части содержит неизвестные постоянные , а числитель левой части -- нет.
Далее можно действовать одним из двух способов: либо, воспользовавшись тем, что числители тождественно равны друг другу, подставлять в тот и в другой некоторые "удобные" значения 
и получать значения постоянных или линейные уравнения, которым они удовлетворяют; либо приравнивать друг к другу коэффициенты при одинаковых степенях в числителях левой и правой частей: эти коэффициенты также совпадают вследствие тождественности числителей. Это также будет давать линейные уравнения, которым должны удовлетворять неизвестные коэффициенты. Оба описанных способа получения соотношений между коэффициентами можно комбинировать друг с другом так, чтобы найти коэффициенты наиболее удобным способом.
Приведём пример.
. Заметим, что в знаменателе этой дроби стоит многочлен , для которого в предыдущем примере мы нашли разложение на множители: 
. Поэтому сумма будет состоять из двух слагаемых: простейшей дроби первого типа, соответствующей линейному множителю 
, и простейшей дроби третьего типа, соответствующей квадратичному множителю . Итак, вид разложения таков:
, состоит из 1 слагаемого; серия, соответствующая 
, также содержит только 1 слагаемое. Через 
и 
обозначены неизвестные пока постоянные. Для нахождения этих постоянных приведём правую часть к общему знаменателю:
, в том числе и при 
. Подставим в левую и правую часть равенства и получим:
откуда
, то есть таких, чтобы какая-либо скобка в правой части обращалась в 0, больше нет, ведь квадратный трёхчлен , как мы проверяли ранее, не имеет вещественных корней. Так что далее мы можем либо подставлять "не вполне удобные" значения , вроде 
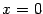
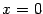
, либо приравнивать друг к другу коэффициенты при одинаковых степенях в левой и правой частях. Пойдём комбинированным путём: сначала подставим (заметим, что это -- то же самое, что приравнять друг к другу свободные члены левой и правой частей):
, получаем:
: в левой части коэффициент равен 5, а в правой, после раскрытия скобок, он оказывается равным 
, так что 
, откуда
Теперь мы можем представить интеграл от дроби в виде:
-- уже не найденный выше коэффициент разложения, а произвольное постоянное слагаемое.) В знаменателе дроби во втором интеграле выделим полный квадрат:
:
, откуда 
и 
, так что этот интеграл приводится к виду 
. Итак,
и 
, получаем окончательно:
, то есть содержит в числителе и знаменателе4 одни лишь чётные степени , то и в правой части разложения достаточно оставить одни лишь чётные относительно слагаемые. Действительно, если дробь имеет вид 
, где 
и 
-- многочлены от переменного 
, то мы можем разложить на сумму простейших дробей правильную дробь 
, а потом подставить в каждом из слагаемых разложения вместо . Очевидно, что тогда все эти слагаемые, зависящие только от , будут чётными функциями. Например, разложение правильной дроби
и 
-- нечётные функции от . Тем самым нам надо будет отыскать всего два неизвестных коэффициента и вместо четырёх: 
и . Точно так же, в случае когда -- нечётная функция от , в искомом разложении можно оставить одни лишь нечётные слагаемые: например, разложение дроби
и 
, коэффициенты которых 
и 
всё равно окажутся равны 0.
Разобранный выше пример 2.11 показывает, что после разложения правильной дроби в сумму простейших дробей интегрирование сводится к интегрированию полученных простейших дробей. Разберём интегрирование всех четырёх типов простейших дробей по порядку.
Интегрирование простейшей дроби первого типа сводится к применению табличной формулы:
Интегрирование простейшей дроби второго типа сводится к табличной формуле после замены вида 
:
Интегрирование простейшей дроби третьего типа выполняется с помощью выделения в знаменателе полного квадрата и разбиения интеграла на два слагаемых, которые вычисляются как было показано выше в примере:
 | |
 |
где
и 
. Осталось подставить 
:
Интегрирование простейшей дроби четвёртого типа также начинается с выделения в знаменателе полного квадрата и замены , после чего интеграл 
приводится к виду 
, где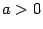 
. Разбиваем этот интеграл на два слагаемых:
:
 | (2.4*) |
 | (2.5) |
Последний интеграл преобразуем, применив формулу интегрирования по частям:
 | |
 |
Подставив это выражение в (2.4*), получаем:
к вычислению интеграла 
. Если 
, то интеграл 
-- табличный; если же 
, то для вычисления нужно снова применить формулу понижения степени, и так до тех пор, пока не получится тот же табличный интеграл 
.
, получаем:
и получим:
 | |
 |
Для вычисления
ещё раз применим тот же самый приём:  | |
 |
Поскольку
 | |
 | |
 |
Приведём теперь пример на интегрирование правильной рациональной дроби общего вида:
Под знаком интеграла -- правильная дробь, поскольку степень числителя, равная 4, меньше степени знаменателя, равной 5. Разложим на множители знаменатель дроби. Это можно сделать, например, группировкой слагаемых:
знаменателя будет соответствовать серия из двух слагаемых, второго и первого типа:
-- одно слагаемое первого типа:
-- одно слагаемое третьего типа:
, так что  | |
 |
Поскольку должны быть тождественно равны эти две дроби с одинаковыми знаменателями, приравниваем числители:
 | |
 |
Из этого соотношения мы должны найти неизвестные коэффициенты
Для этого сначала используем подстановку "удобных" значений , то есть 
и , которые обращают в 0 скобки 
и 
соответственно. При получаем: 
откуда
получаем: 
откуда
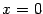
нет. Подставим , то есть приравняем свободные члены левой и правой частей: 
С учётом того, что 
и 
, получаем уравнение
в левой и правой частях. Приравниваем коэффициенты при 
: 
С учётом получаем второе уравнение:
: 
или
:
 | |
 | |
 | |
 |
Заметим, что ввиду того, что подынтегральная функция имеет разрывы при
и , слагаемое означает в данной формуле кусочно постоянную функцию, принимающую постоянные (но, может быть, различные) значения на интервалах 
, 
и 
.
