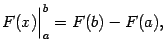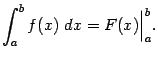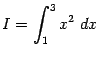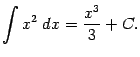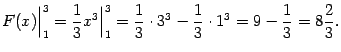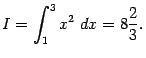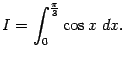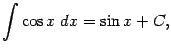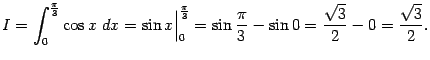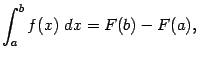‹-- Назад
Интеграл с переменным верхним пределом
Рассмотрим функцию ![]() , заданную на отрезке
, заданную на отрезке ![]() , и предположим, что она интегрируема на отрезке
, и предположим, что она интегрируема на отрезке ![]() . Тогда при любом
. Тогда при любом ![]() эта функция будет интегрируема на отрезке
эта функция будет интегрируема на отрезке ![]() и, следовательно, функция
и, следовательно, функция
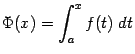
Доказательство. Заметим, что если функция ![]() положительна, то значение
положительна, то значение ![]() интерпретируется как площадь под графиком
интерпретируется как площадь под графиком ![]() , лежащая над отрезком
, лежащая над отрезком ![]() . Если дать
. Если дать ![]() приращение
приращение ![]() , то площадь получит приращение в виде площади полоски, лежащей над отрезком
, то площадь получит приращение в виде площади полоски, лежащей над отрезком ![]() (см. рис.).
(см. рис.).
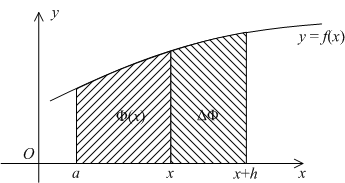
Эта площадь, вследствие ограниченности интегрируемой функции, мала, если приращение
Проведём теперь более аккуратные рассуждения, не предполагая, что функция принимает положительные значения.
Пусть фиксирована точка ![]() и взято такое приращение
и взято такое приращение ![]() , что
, что ![]() . Пользуясь аддитивностью интеграла, получаем, что
. Пользуясь аддитивностью интеграла, получаем, что
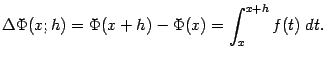
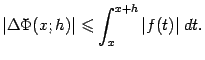
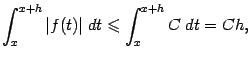
Рассматривая аналогично отрезок ![]() при
при ![]() и
и ![]() , получаем, что
, получаем, что
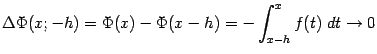
Тем самым функция ![]() непрерывна справа в точке
непрерывна справа в точке ![]() , непрерывна слева в точке
, непрерывна слева в точке ![]() и непрерывна (с обеих сторон) в любой точке
и непрерывна (с обеих сторон) в любой точке ![]() , что и требовалось доказать.
, что и требовалось доказать.
Доказательство. Снова рассмотрим приращение ![]() при
при ![]() ,
, ![]() ,
, ![]() . Поскольку функция
. Поскольку функция ![]() непрерывна, мы можем применить теорему о среднем к интегралу по отрезку
непрерывна, мы можем применить теорему о среднем к интегралу по отрезку ![]() :
:
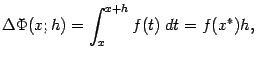
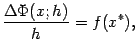
Аналогично доказывается, что левая производная ![]() совпадает с
совпадает с ![]() во всех точках
во всех точках ![]() Во внутренних точках
Во внутренних точках ![]() совпадение производных слева и справа со значением
совпадение производных слева и справа со значением ![]() означает, что функция
означает, что функция ![]() имеет производную
имеет производную ![]() , равную
, равную ![]() .
.
Точно так же доказывается, что производная интеграла
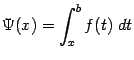
Равенство ![]() означает, что функция
означает, что функция ![]() является первообразной для
является первообразной для ![]() на интервале
на интервале ![]() . Другая первообразная -- это, очевидно, функция
. Другая первообразная -- это, очевидно, функция ![]() .
.
Итак, мы получили важный результат о наличии первообразной у любой непрерывной функции:
Доказательство. Для доказательства достаточно фиксировать произвольную точку ![]() и положить
и положить
Нетрудно видеть, что при ![]() получается
получается ![]() , при
, при ![]() получаем
получаем ![]() . При
. При ![]() производная слева даёт значение
производная слева даёт значение ![]() , а производная справа -- значение
, а производная справа -- значение ![]() , так что производные слева и справа совпадают и
, так что производные слева и справа совпадают и ![]() , что и завершает доказательство.
, что и завершает доказательство.
Пусть теперь ![]() -- произвольная первообразная для непрерывной функции
-- произвольная первообразная для непрерывной функции ![]() , заданной на некотором интервале
, заданной на некотором интервале ![]() , содержащем отрезок
, содержащем отрезок ![]() . Мы уже проверили, что функция
. Мы уже проверили, что функция ![]() , такая что
, такая что ![]() при
при ![]() служит тогда первообразной для
служит тогда первообразной для ![]()
![]() , а поскольку любые первообразные для одной и той же функции на заданном интервале могут отличаться лишь постоянным слагаемым, получаем, что
, а поскольку любые первообразные для одной и той же функции на заданном интервале могут отличаться лишь постоянным слагаемым, получаем, что
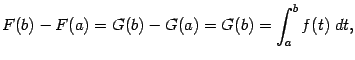
где
Напомним, что мы получили её в предположении, что функция ![]() непрерывна. Если функция
непрерывна. Если функция ![]() имеет разрыв на отрезке
имеет разрыв на отрезке ![]() , то разность значений первообразной может не иметь никакого отношения к величине определённого интеграла. Поэтому при применении формулы Ньютона - Лейбница нужно строго следить за законностью этого действия.
, то разность значений первообразной может не иметь никакого отношения к величине определённого интеграла. Поэтому при применении формулы Ньютона - Лейбница нужно строго следить за законностью этого действия.
Смысл формулы Ньютона - Лейбница (3.6) состоит в том, что для нахождения определённого интеграла ![]() нам достаточно теперь найти произвольную первообразную
нам достаточно теперь найти произвольную первообразную ![]() для функции
для функции ![]() (напомним, что для этого надо найти неопределённый интеграл) и взять разность значений этой первообразной в концах отрезка,
(напомним, что для этого надо найти неопределённый интеграл) и взять разность значений этой первообразной в концах отрезка, ![]() .
.
Итак, формула Ньютона - Лейбница устанавливает связь между определённым интегралом от данной функции и первообразной для этой функции, то есть между определённым и неопределённым интегралами. Заметим, что смысл этих двух понятий первоначально совершенно различен: неопределённый интеграл -- это набор функций (первообразных), а определённый интеграл -- это число (равное пределу интегральных сумм).
При вычислениях разность ![]() часто называют подстановкой в функцию
часто называют подстановкой в функцию ![]() пределов
пределов ![]() и
и ![]() и обозначают
и обозначают 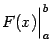 . Таким образом, по определению,
. Таким образом, по определению,