‹-- Назад
Два коэффициента при переменных равны нулю
В соответствии с подразделом "Один из коэффициентов при неизвестных равен нулю" плоскость должна быть параллельна каждой из осей отсутствующих переменных и, следовательно, параллельна координатной плоскости, содержащей эти оси. Тогда можно найти точку
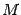
пересечения исходной плоскости с осью переменного, явно присутствующего в ее уравнении, и провести через нее прямые, параллельные двум другим осям. Например, построим изображение плоскости 
. Плоскость параллельна оси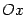 
и оси 
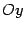. Следовательно, плоскость параллельна координатной плоскости 
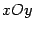. Находим точку 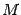пересечения исходной плоскости с осью 
: 
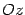. Проводим через точку 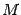две прямые, параллельные осям 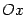и 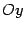, соответственно. Получаем изображение плоскости (рис. 11.5).
Упражнение11.3.1. Постройте плоскость 
. После выполнения построений можете посмотреть один из вариантов правильного чертежа здесь.
Упражнение11.3.2. Постройте плоскость
. После выполнения построений можете посмотреть один из вариантов правильного чертежа здесь.
Упражнение11.3.3. Постройте плоскость
. После выполнения построений можете посмотреть один из вариантов правильного чертежа здесь.
Упражнение11.3.4. Постройте плоскость
. После выполнения построений можете посмотреть один из вариантов правильного чертежа здесь. 