‹-- Назад Теперь, после изучения формулы Ньютона - Лейбница, мы можем, в принципе, найти определённый интеграл для любой функции, для которой умеем вычислить неопределённый интеграл, и для этого не нужно никаких дополнительных формул и правил. Однако для уменьшения громоздкости вычисления некоторых интегралов, полезно получить формулы для определённого интеграла в тех случаях, когда приходится применять замену переменного или формулу интегрирования по частям.
Формула замены переменного в определённом интеграле.
Доказательство. Пусть  -- некоторая первообразная для
-- некоторая первообразная для  , так что
, так что
и

-- некоторая первообразная для

, так что
Поскольку по теореме о замене переменного в неопределённом интеграле имеет место формула
то есть
где

, то при

и

имеем

и

, откуда
Учитывая, что

и

, получаем
а это и есть доказываемая формула замены переменного.
Замечание 3.4 Заметим, что доказанная формула, в отличие от формулы замены переменной в неопределённом интеграле, даёт нам возможность после перехода к интегралу от функции новой переменной
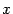
не возвращаться к исходному интегралу от функции переменной

. После того, как замена сделана, мы можем "забыть", как выглядел исходный интеграл, и продолжать преобразования интеграла от функции новой переменной. Именно на том, что к старой переменной возвращаться не приходится, мы и получаем экономию усилий при применении формулы замены переменной в определённом интеграле, по сравнению с тем, что получилось бы, если бы мы просто нашли первообразную и применили формулу Ньютона - Лейбница.
Обратим ваше внимание на важную особенность формулы: кроме подынтегрального выражения, при замене переменной меняются и пределы интегрирования. Действительно, в интеграле по новой переменной 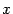 должны быть указаны пределы изменения именно
должны быть указаны пределы изменения именно 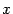 (то есть
(то есть  и
и  ), в то время как в исходном интеграле по переменной
), в то время как в исходном интеграле по переменной  указаны пределы изменения
указаны пределы изменения  (то есть
(то есть  и
и  )!
)!
Советы о том, какая замена целесообразна для вычисления того или иного интеграла, -- те же самые, что и при вычислении неопределённых интегралов, так что тут ничего нового изучать не придётся.
Пример 3.3 Вычислим интеграл
Для этого сделаем замену

, откуда

. Кроме того, при

имеем

, а при

имеем

. Получаем:
Формула интегрирования по частям для определённого интеграла.
Замечание 3.5 Заметим, что эту формулу можно записать в виде
где выражение
называется
внеинтегральным членом. Введя обозначения

и

, мы можем переписать формулу интегрирования по частям в более коротком виде:
Доказательство теоремы 3.15. Поскольку из условий теоремы следует, что под знаками интегралов в левой и правой частях равенства стоят непрерывные функции, то к этим интегралам можно применять формулу Ньютона - Лейбница:
и
Пусть  -- некоторая первообразная для функции
-- некоторая первообразная для функции  , а
, а  -- некоторая первообразная для функции
-- некоторая первообразная для функции  . Формула интегрирования по частям для неопределённого интеграла, то есть
. Формула интегрирования по частям для неопределённого интеграла, то есть
означает, что
где

. Положим теперь

и

и получим:

и

, откуда
Но с учётом равенств, полученных выше по формуле Ньютона - Лейбница, это как раз и даёт доказываемую формулу.
Замечание 3.6 Советы, в каких случаях целесообразно применять формулу интегрирования по частям, остаются теми же, как в случае вычисления неопределённых интегралов. Выигрыш от применения формулы интегрирования по частям для определённого интеграла по сравнению с предварительным вычислением первообразной по формуле интегрирования по частям для неопределённого интеграла, а затем применением формулы Ньютона - Лейбница получается от того, что мы сразу, при возникновении внеинтегрального члена, можем вычислить подстановку и далее при преобразованиях использовать полученное число вместо выражения, задающего внеинтегральный член.
Пример 3.4 Вычислим интеграл
Выгодно взять

и

, так что получаем:
При этом возникший по дороге внеинтегральный член

мы вычислили так:
Особенно ясно проявляется указанное в замечании преимущество в том случае, если формулу интегрирования по частям приходится применять несколько раз подряд.
Пример 3.5 Вычислим интеграл
применив формулу интегрирования по частям два раза подряд. Имеем:
Если бы мы сразу же не вычисляли значения подстановок во внеинтегральных членах, то нам пришлось бы несколько раз при нахождении первообразных выписывать значения этих внеинтегральных членов

и

, а здесь мы сразу же заменили первую подстановку на 0, а вторую на

, что сэкономило некоторое место в записи и наши усилия.
Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции

![]() -- некоторая первообразная для
-- некоторая первообразная для ![]() , так что
, так что 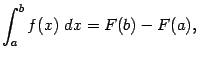


![]() должны быть указаны пределы изменения именно
должны быть указаны пределы изменения именно ![]() (то есть
(то есть ![]() и
и ![]() ), в то время как в исходном интеграле по переменной
), в то время как в исходном интеграле по переменной ![]() указаны пределы изменения
указаны пределы изменения ![]() (то есть
(то есть ![]() и
и ![]() )!
)! 






![]() -- некоторая первообразная для функции
-- некоторая первообразная для функции ![]() , а
, а ![]() -- некоторая первообразная для функции
-- некоторая первообразная для функции ![]() . Формула интегрирования по частям для неопределённого интеграла, то есть
. Формула интегрирования по частям для неопределённого интеграла, то есть 




 мы вычислили так:
мы вычислили так: 



