‹-- Назад Дадим теперь определение точек разрыва функции.
Определение 3.2 Точка

называется
точкой разрыва функции

, если она определена в некоторой проколотой окрестности точки

(то есть определена на некотором интервале, для которого

служит внутренней точкой, но в самой точке

, возможно, не определена) и выполняется хотя бы одно из следующих условий:
1) не существует предела слева  ;
;
2) не существует предела справа  ;
;
3) пределы слева  и справа
и справа  существуют, но не равны друг другу:
существуют, но не равны друг другу:  ;
;
4) пределы слева  и справа
и справа  существуют и равны друг другу:
существуют и равны друг другу:  , но не совпадают со значением функции в точке
, но не совпадают со значением функции в точке  :
:  , или функция
, или функция  не определена в точке
не определена в точке  .
.
Если имеет место либо случай 3, либо случай 4, то точка разрыва  называется точкой разрыва первого рода, а поведение функции в окрестности точки
называется точкой разрыва первого рода, а поведение функции в окрестности точки  называется разрывом первого рода в точке
называется разрывом первого рода в точке  ; в случае 4 точка разрыва первого рода называется устранимой точкой разрыва, а разрыв функции в этой точке -- устранимым разрывом.
; в случае 4 точка разрыва первого рода называется устранимой точкой разрыва, а разрыв функции в этой точке -- устранимым разрывом.
Если же имеет место либо случай 1, либо случай 2 (либо и тот и другой сразу), то точка разрыва  называется точкой разрыва второго рода, а поведение функции в окрестности этой точки -- разрывом второго рода в точке
называется точкой разрыва второго рода, а поведение функции в окрестности этой точки -- разрывом второго рода в точке  .
.
Итак, если функция  имеет разрыв первого рода в точке
имеет разрыв первого рода в точке  , то существуют, как часто говорят, значения функции "на берегах разрыва":
, то существуют, как часто говорят, значения функции "на берегах разрыва":  и
и  , но точка
, но точка  не является точкой непрерывности.
не является точкой непрерывности.

Рис.3.2. -- точка разрыва первого рода
-- точка разрыва первого рода Если значения на берегах разрыва разные, то значение функции в точке  может быть любым (или вообще отсутствовать), всё равно
может быть любым (или вообще отсутствовать), всё равно  будет давать разрыв первого рода. Если же значения на берегах разрыва совпадают, то для наличия разрыва нужно, чтобы либо эти совпадающие значения были отличны от значения функции в точке
будет давать разрыв первого рода. Если же значения на берегах разрыва совпадают, то для наличия разрыва нужно, чтобы либо эти совпадающие значения были отличны от значения функции в точке  , либо функция в этой точке была вовсе не определена. Если в этом случае переопределить (или доопределить) функцию
, либо функция в этой точке была вовсе не определена. Если в этом случае переопределить (или доопределить) функцию  в точке
в точке  , положив
, положив  , то полученная изменённая функция будет уже непрерывна в точке
, то полученная изменённая функция будет уже непрерывна в точке  и разрыв в точке
и разрыв в точке  исчезнет; отсюда и название такого разрыва -- устранимый.
исчезнет; отсюда и название такого разрыва -- устранимый.

Рис.3.3. -- точка устранимого разрыва
-- точка устранимого разрыва Наконец, к разрывам второго рода, как видно из определения, относятся все разрывы, которые не принадлежат к разрывам первого рода; некоторые из возможных способов поведения функции в окрестности точки  , где происходит разрыв второго рода, представлены на следующем рисунке.
, где происходит разрыв второго рода, представлены на следующем рисунке.



Рис.3.4. -- точка разрыва второго рода. Некоторые возможные варианты
-- точка разрыва второго рода. Некоторые возможные варианты
Пример 3.3 Рассмотрим функцию

, для которой
Функция имеет разрывы при

и при

. Нетрудно видеть, что при


В точках

и

функция имеет неустранимые разрывы первого рода. В точке

имеем:
(значения на краях разыва существуют, но не совпадают); в точке

--
(снова пределы слева и справа существуют, но не совпадают).

Рис.3.5.График функции 
Пример 3.4 Функция
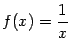
имеет при

разрыв второго рода, так как

при

и

при

.

Рис.3.6.График функции 
Пример 3.5 Функция
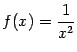
имеет при

разрыв второго рода, так как

при

и при

.

Рис.3.7.График функции 
Пример 3.6 Возьмём

. Все точки области определения

этой элементарной функции являются точками непрерывности. Поскольку
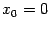
не входит в область определения функции

, но

определена во всех точках любой проколотой окрестности 0, то 0 -- точка разрыва функции

. Разобранный выше
пример 3.2 показывает, что если доопределить эту функцию при
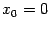
, положив

, то функция становится непрерывной в точке 0. Значит, 0 -- точка разрыва первого рода для функции

.

Рис.3.8.Устранимый разрыв функции 
Пример 3.7 Рассмотрим функцию

. Её область определения

состоит из точек непрерывности, так как это элементарная функция. Точка
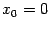
, в которой функция не определена, -- это точка разрыва функции. Поскольку

при

, то

. Это означает, что при

функция имеет устранимый разрыв и становится непрерывной на всей вещественной оси, если положить

.

Рис.3.9.Устранимый разрыв функции 
Пример 3.8 Рассмотрим функцию

, где

. При

она имеет разрыв, так как

. Поскольку

-- ограниченная функция, а

при

, то

(по
теореме 2.7). Следовательно, разрыв устранимый, и если доопределить функцию, положив

, она становится непрерывной при всех

.

Рис.3.10.График функции  при
при 
Пример 3.9 Рассмотрим функцию

, заданную равенством
При

,

,

, так что последовательность

-- это геометрическая прогрессия со знаменателем

,

, и

При

,

,

, и все

, так что

При

,

,

, и последовательность имеет вид
Эта последовательность предела не имеет, так что функция

не определена при

,

.

Рис.3.11.График функции 
Получаем, что  . Точками разрыва этой функции служат как все точки, не принадлежащие области определения (точки вида
. Точками разрыва этой функции служат как все точки, не принадлежащие области определения (точки вида  ,
,  ), так и все точки вида
), так и все точки вида  ,
,  , в которых функция принимает значение 1. Все точки разрыва -- устранимые, так как пределы функции слева и справа в этих точках совпадают и равны 0.
, в которых функция принимает значение 1. Все точки разрыва -- устранимые, так как пределы функции слева и справа в этих точках совпадают и равны 0.
Пример 3.10 Рассмотрим функцию

; её область определения

, и точка

-- точка разрыва. Рассмотрим поведение функции слева и справа от точки разрыва. При

будет

и

; при

будет

и

. Итак, значения "на правом берегу" разрыва не существует, и разрыв функции

в точке

-- второго рода.

Рис.3.12.График функции 
Замечание 3.1 Если функция

не определена на интервале, примыкающем к точке

слева или справа, то точку

мы не считаем точкой разрыва функции.
Пример 3.11 Рассмотрим функцию

. Её область определения --

. При

и при

знаменатель

стремится к 0 и положителен, так что

. однако точки

и

мы не считаем точками разрыва, так как функция

не определена при

и при

.

Рис.3.13.График функции 
Пример 3.12 Рассмотрим функцию

. Её область определения -- это

. Точка

не является точкой разрыва функции

, несмотря на характер её поведения при

, поскольку функция

не определена при

.

Рис.3.14.График функции 
Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции
![]() ;
; ![]() ;
; ![]() и справа
и справа ![]() существуют, но не равны друг другу:
существуют, но не равны друг другу: ![]() ;
; ![]() и справа
и справа ![]() существуют и равны друг другу:
существуют и равны друг другу: ![]() , но не совпадают со значением функции в точке
, но не совпадают со значением функции в точке ![]() :
: ![]() , или функция
, или функция ![]() не определена в точке
не определена в точке ![]() .
. ![]() называется точкой разрыва первого рода, а поведение функции в окрестности точки
называется точкой разрыва первого рода, а поведение функции в окрестности точки ![]() называется разрывом первого рода в точке
называется разрывом первого рода в точке ![]() ; в случае 4 точка разрыва первого рода называется устранимой точкой разрыва, а разрыв функции в этой точке -- устранимым разрывом.
; в случае 4 точка разрыва первого рода называется устранимой точкой разрыва, а разрыв функции в этой точке -- устранимым разрывом. ![]() называется точкой разрыва второго рода, а поведение функции в окрестности этой точки -- разрывом второго рода в точке
называется точкой разрыва второго рода, а поведение функции в окрестности этой точки -- разрывом второго рода в точке ![]() .
. ![]() имеет разрыв первого рода в точке
имеет разрыв первого рода в точке ![]() , то существуют, как часто говорят, значения функции "на берегах разрыва":
, то существуют, как часто говорят, значения функции "на берегах разрыва": ![]() и
и ![]() , но точка
, но точка ![]() не является точкой непрерывности.
не является точкой непрерывности. 
![]() может быть любым (или вообще отсутствовать), всё равно
может быть любым (или вообще отсутствовать), всё равно ![]() будет давать разрыв первого рода. Если же значения на берегах разрыва совпадают, то для наличия разрыва нужно, чтобы либо эти совпадающие значения были отличны от значения функции в точке
будет давать разрыв первого рода. Если же значения на берегах разрыва совпадают, то для наличия разрыва нужно, чтобы либо эти совпадающие значения были отличны от значения функции в точке ![]() , либо функция в этой точке была вовсе не определена. Если в этом случае переопределить (или доопределить) функцию
, либо функция в этой точке была вовсе не определена. Если в этом случае переопределить (или доопределить) функцию ![]() в точке
в точке ![]() , положив
, положив ![]() , то полученная изменённая функция будет уже непрерывна в точке
, то полученная изменённая функция будет уже непрерывна в точке ![]() и разрыв в точке
и разрыв в точке ![]() исчезнет; отсюда и название такого разрыва -- устранимый.
исчезнет; отсюда и название такого разрыва -- устранимый. 
![]() , где происходит разрыв второго рода, представлены на следующем рисунке.
, где происходит разрыв второго рода, представлены на следующем рисунке. 


 , для которой
, для которой  В точках
В точках 
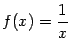 имеет при
имеет при 
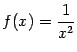 имеет при
имеет при 

 при
при 


![]() . Точками разрыва этой функции служат как все точки, не принадлежащие области определения (точки вида
. Точками разрыва этой функции служат как все точки, не принадлежащие области определения (точки вида ![]() ,
, ![]() ), так и все точки вида
), так и все точки вида ![]() ,
, ![]() , в которых функция принимает значение 1. Все точки разрыва -- устранимые, так как пределы функции слева и справа в этих точках совпадают и равны 0.
, в которых функция принимает значение 1. Все точки разрыва -- устранимые, так как пределы функции слева и справа в этих точках совпадают и равны 0. 
 . Её область определения --
. Её область определения -- 

 . Её область определения -- это
. Её область определения -- это 
