‹-- Назад
Бесконечно малые и локально ограниченные величины и их свойства
В этом разделе мы изучим свойства бесконечно малых величин, то есть величин, стремящихся к 0. В следующих разделах на этой основе мы будем изучать свойства величин, имеющих произвольное значение предела.
называется бесконечно малой величиной при базе 
, если её предел при данной базе равен 0, то есть 
.
Заметим, что в этом определении фигурирует фиксированная база ; в зависимости от того, какая именно база взята, одна и та же функция может как быть бесконечно малой, так и не быть ею.
. При базе 
эта функция является бесконечно малой, а при базе 
-- не является. 
Проверим это. Покажем, что 
. Возьмём произвольное 
и решим неравенство 
. Оно эквивалентно неравенству 
. Получаем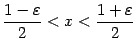 
; это означает, что при 
, где 
, неравенство выполняется, то есть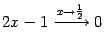 
. Мы показали, что 
-- бесконечно малая при 
.
Теперь покажем, что 
, то есть что эта величина не является бесконечно малой при . Возьмём 
и найдём окрестность точки 0, в которой выполняется неравенство 
. Это неравенство, очевидно, эквивалентно неравенству 
, то есть при 
попадание 
в 
-окрестность точки 0 гарантирует выполнение неравенства . Это означает, что 
.
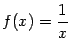-- бесконечно малая при 
, 
и при 
. Для того, чтобы это доказать, достаточно для любого указать окончание 
базы , на котором выполняется неравенство 
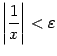. При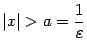 
, очевидно, неравенство выполняется. Это означает, что 
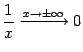. Докажем теперь теорему, связывающую бесконечно малые с величинами, имеющими произвольное значение предела.
имеет при базе предел, равный 
, тогда и только тогда, когда величина 
является бесконечно малой при базе : 
Доказательство. Согласно определению предела, равенство 
означает, что для любого можно найти такое окончание 
, что
при всех Условие
означает, что для любого можно найти такое окончание , что  при всех  |
Но это, очевидно, то же, что формула (2.1).
Теперь обратимся к свойствам, касающимся собственно бесконечно малых.
и 
-- бесконечно малые при одной и той же базе . Тогда и их сумма 
-- тоже бесконечно малая при базе . Доказательство. Пусть фиксировано некоторое число . Рассмотрим положительное число 
. Условие 
означает, что найдётся такое окончание 
, на котором 
меньше этого положительного числа: 
при всех 
.
Точно так же, условие 
означает, что найдётся такое окончание 
, на котором 
при всех 
. По определению базы, она содержит некоторое окончание 
. Так как 
-- часть как 
, так и 
, то оба неравенства выполняются при 
. Тогда при будет
мы предъявили такое окончание 
, на котором выполняется неравенство 
. Это означает, что 
, то есть что 
-- бесконечно малая при базе .
рассмотрим две бесконечно малых величины: 
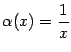и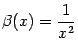 
. Вместе с ними и величина 
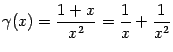тоже является бесконечно малой при базе . Докажем теперь, как следствие из предыдущей теоремы, утверждение о том, что бесконечно малой является сумма не только двух, но любого числа бесконечно малых величин.
-- бесконечно малые при базе , 
. Тогда величина 
. Доказательство. Доказывать утверждение теоремы мы будем по индукции5 по числу слагаемых. Для двух слагаемых это утверждение верно по теореме 2.5. Пусть утверждение верно для 
слагаемых; это означает, что величина 
бесконечно мала. Покажем, что тогда оно верно и для 
слагаемых. По условию бесконечно мала также величина 
и, значит, по теореме 2.5 бесконечно мала сумма этих двух бесконечно малых 
. Тем самым шаг индукции сделан и утверждение доказано для произвольного числа слагаемых .
В дальнейшем нам часто будет нужно рассматривать функции, которые не превосходят некоторой постоянной на некотором окончании данной базы. Дадим им следующее название.
называется локально ограниченной при базе , если она определена на некотором окончании 
этой базы и существует такая постоянная 
, что 
при всех 
. 
локально ограничена при любой базе. Действительно, в качестве ограничивающей постоянной достаточно взять 
; тогда условие 
верно для из любого окончания 
любой базы . Докажем следующее утверждение, имеющее вспомогательный характер для дальнейшего.
две функции и 
являются локально ограниченными. Тогда и их произведение тоже локально ограничено при этой базе. Доказательство. Из условия следует, что 
при и 
при , где 
-- некоторые постоянные и 
-- некоторые окончания базы . Возьмём окончание ; при будут выполнены оба неравенства и, следовательно,
служит ограничивающей постоянной для произведения 
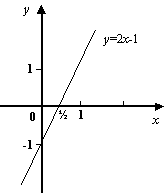
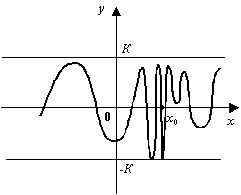
на окончании , то есть это произведение локально ограничено при базе . Локальная ограниченность функции не означает, что она ограничена на всей своей области определения. Например, функция 
локально ограничена при базе , но не является ограниченной функцией при всех 
. Если в качестве базы рассматривается , то локальная ограниченность функции при этой базе означает, что функция ограничена в некоторой, быть может, достаточно малой, окрестности точки 
.
имеет предел при базе . Тогда эта функция локально ограничена при этой базе. Доказательство. Пусть ; это означает, что при любом (возьмём, например, 
) найдётся такое окончание базы , что 
для любого 
. Тем самым, при выполнено двойное неравенство 
.
Выберем из двух чисел 
и 
число с большей абсолютной величиной и обозначим его : 
. Тогда, очевидно, из последнего неравенства следует, что 
; это означает, что функция локально ограничена.
В частности, локально ограничены при базе все бесконечно малые при базе , так как все они, по определению, имеют предел (равный 0).
и базу . Локальная ограниченность функции очевидна: можно взять постоянную 
и окончание базы 
, тогда 
при всех 
. Однако 
не имеет предела при : какое бы окончание 
ни взять, при 
значения многократно изменяются от 
до 1 и назад и не приближаются ни к какому постоянному значению. (В качестве упражнения проведите строгое доказательство того, что предел 
не существует: докажите, что при 
нельзя указать окончания базы 
, при всех из которого при некотором выполнялось бы неравенство 
. Такое окончание 
должно было бы существовать по определению предела, если бы предел существовал.) Поскольку предела при не существует, то если сделать замену 
, получится, что предел 
также не существует. График функции 
представлен на следующем рисунке.
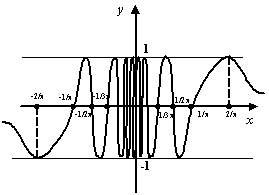
График совершает бесконечно много колебаний при подходе к 0. Размах каждого колебания остаётся один и тот же, от до 1. Значения, равные 1, функция принимает в точках вида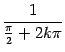 
, 
, значения, равные , -- в точках вида 
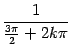, , а значения, равные 0, -- в точках вида 
, .
Докажем теперь теорему о взаимосвязи локально ограниченных и бесконечно малых величин.
-- база, функция локально ограничена, а функция бесконечно мала при этой базе. Тогда их произведение 
-- бесконечно малая при базе . Доказательство. Так как локально ограничена при базе , то при некотором 
и всех из некоторого окончания базы . Фиксируем произвольное число и рассмотрим положительное число 
. Так как -- бесконечно малая при базе , то найдётся такое окончание , что при всех выполняется неравенство 
. Рассмотрим теперь некоторое окончание 
. (Такое окончание существует по определению базы.) Так как -- часть как , так и , то при выполняются одновременно неравенства и 
, из которых следует, что 
при всех . Так как число было выбрано произвольно, это означает, что функция является бесконечно малой при базе .
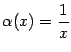и . Так как бесконечно мала, а локально ограничена при базе , то их произведение 
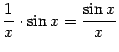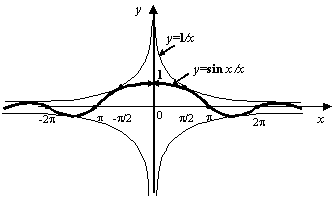
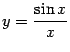
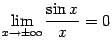-- бесконечно малая при , а также при и при (см. упражнение 2.4). 
. Тогда, очевидно, функция 
перейдёт в функцию 
, а базы , и , соответственно, в базы 
, 
и 
. Значение предела 
при замене не изменится, так что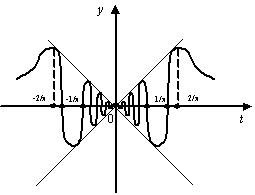 
-- постоянная и -- бесконечно малая при базе . Тогда 
-- тоже бесконечно малая при базе . Доказательство. Достаточно заметить, что локально ограничена при базе и сослаться на предыдущую теорему.
-- бесконечно малые при базе и 
-- произвольные постоянные. Тогда величина вида 
. Доказательство. Чтобы доказать это следствие, достаточно заметить, что все слагаемые являются бесконечно малыми, согласно предыдущему следствию, а затем применить утверждение следствия 2.1.
всех функций, определённых на некотором фиксированном окончании базы и бесконечно малых при этой базе , имеет структуру линейного пространства: любые элементы этого пространства можно умножать на постоянные и складывать, не выходя за рамки этого пространства.
