‹-- Назад
Равномерная непрерывность
Напомним, что непрерывность функции
в точке 
означает, что 
, то есть 
Тем самым непрерывность функции
на интервале или отрезке 
означает, что 
При этом мы имеем право выбирать число
в зависимости от 
и, главное, от точки 
. Предположим теперь, что число можно выбрать общим для всех (но, конечно, зависящим от ). Тогда говорят, что свойство функции быть непрерывной в точке выполнено равномерно по .
Дадим теперь такое
-- некоторая функция и . Функция равномерно непрерывна на 
, если 
Приведём пример равномерно непрерывной функции.
и покажем, что она равномерно непрерывна на всей числовой оси 
. Фиксируем число 
и положим 
. Выберем теперь любые две точки 
и , такие что 
, и покажем, что тогда 
. Действительно,  |
так как, во-первых,
при всех и и, во-вторых, 
при всех 
(у нас 
). Таким образом. равномерная непрерывность функции 
доказана. Лучше изучить условие равномерности по мы сможем, приведя пример, где оно нарушается.
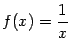рассматривается на интервале 
. Если фиксирована точка 
, то для заданного мы можем выбрать так, что 
при всех таких, что 
; для нахождения 
нужно решить неравенство относительно (напомним, что точка фиксирована):  | |
 |
Из чисел
и 
выберем минимальное: 
будет . Проанализируем, однако, зависимость от : при , приближающемся к 0, значения 
будут убывать и стремиться к 0 (при неизменном значении ), что хорошо видно на следующем чертеже: 
в зависимости от положения точки При приближении точки к началу координат нам приходится по одному и тому же выбирать всё меньшие -окрестности точки , чтобы обеспечить выполнение неравенства . Выбрать общим для всех , очевидно, невозможно: при заданном какое бы фиксированное число ни было взято, мы можем поместить точку так близко от 0, что значения 
и 
будут отличаться друг от друга больше, чем на , хотя . Это означает, что функция 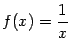не является равномерно непрерывной на интервале .
и функция непрерывна на . Тогда равномерно непрерывна на . Доказательство этой теоремы достаточно сложно и основывается на тонких свойствах системы действительных чисел, а именно, на том, что любой замкнутый отрезок является компактом9. Мы пропускаем здесь доказательство теоремы, отсылая за ним заинтересованного читателя к подробным курсам математического анализа, например, Никольский С.М., Курс математического анализа, т. 1. -- М.: Наука, 1991; Фихтенгольц Г.М., Курс дифференциального и интегрального исчисления, т. 1. -- М.-Л.: ГИТТЛ, 1948 и др. годы изд.
В качестве следствия равномерной непрерывности легко получается утверждение теоремы 3.8, а именно,
, непрерывная на замкнутом отрезке 
, ограничена на (то есть существует такое число 
, что 
при всех 
). Приведём это доказательство (хотя теорема 3.8 была ранее доказана другим способом):
Доказательство. Фиксируем какое-либо число , например 
, и выберем такое, что при всех 
, для которых , будет 
. Разобьём на отрезки длины 
:
;10 длина последнего отрезка может оказаться меньше ). Выберем в качестве середину 
каждого из отрезков: 
выполняется неравенство 
и, следовательно, 
. Это неравенство эквивалентно такому: 
, или 
. Поскольку точек конечное число (а именно, 
), то мы можем взять минимальное из чисел 
, 
, и максимальное из чисел 
, : 
верно неравенство 
, и осталось взять 
. При этом для любого будет , что означает ограниченность функции на .
