‹-- Назад Самый простой метод приближённого вычисления площадей узких полосок -- заменить их площадями
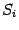
прямоугольников, основанием которых служит отрезок
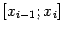
на оси

, а высотой -- отрезок, задающий значение функции в одном из концов основания, то есть либо в точке

, либо в точке
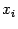
. Тогда в первом случае площадь
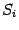
равняется

, а во втором

.
Суммируя по всем отрезкам разбиения, то есть по 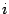 от
от  до
до  , получаем в первом случае квадратурную формулу левых прямоугольников:
, получаем в первом случае квадратурную формулу левых прямоугольников:
а во втором случае
квадратурную формулу левых прямоугольников:

Рис.5.2.
Из приведённого чертежа ясно, что ошибки

и

, которые возникают при замене точного значения интеграла

на его приближённое значение

или

соответственно, обладают такими свойствами:
если функция  возрастает на
возрастает на 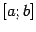 , то
, то  , поскольку
, поскольку  ;
;
если функция  убывает на
убывает на 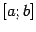 , то
, то  , поскольку
, поскольку  ;
;
если функция  возрастает на
возрастает на 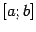 , то
, то  , поскольку
, поскольку  ;
;
если функция  убывает на
убывает на 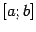 , то
, то  , поскольку
, поскольку  .
.
Таким образом, в случае монотонной функции 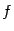 ошибки
ошибки  и
и  имеют разные знаки. Возникает желание взаимно скомпенсировать эти ошибки (хотя бы частично), взяв полусумму чисел
имеют разные знаки. Возникает желание взаимно скомпенсировать эти ошибки (хотя бы частично), взяв полусумму чисел  и
и  за приближённое значение интеграла. Получаем при этом такую квадратурную формулу:
за приближённое значение интеграла. Получаем при этом такую квадратурную формулу:
Как мы впоследствии увидим, полученная квадратурная формула в точности совпадает с
формулой трапеций. Она часто применяется на практике для вычисления интеграла благодаря своей простоте. Сами же формулы для

и

, из которых она возникла, на практике при=меняются чрезвычайно редко ввиду своей малой точности: ошибки

и

слишком значительны даже при достаточно мелких разбиениях. Гораздо большую точность обеспечивает следующий метод, применение которого ничуть не сложнее.
Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции
![]() от
от ![]() до
до ![]() , получаем в первом случае квадратурную формулу левых прямоугольников:
, получаем в первом случае квадратурную формулу левых прямоугольников: 


![]() возрастает на
возрастает на ![]() , то
, то ![]() , поскольку
, поскольку ![]() ;
; ![]() убывает на
убывает на ![]() , то
, то ![]() , поскольку
, поскольку ![]() ;
; ![]() возрастает на
возрастает на ![]() , то
, то ![]() , поскольку
, поскольку ![]() ;
; ![]() убывает на
убывает на ![]() , то
, то ![]() , поскольку
, поскольку ![]() .
. ![]() ошибки
ошибки ![]() и
и ![]() имеют разные знаки. Возникает желание взаимно скомпенсировать эти ошибки (хотя бы частично), взяв полусумму чисел
имеют разные знаки. Возникает желание взаимно скомпенсировать эти ошибки (хотя бы частично), взяв полусумму чисел ![]() и
и ![]() за приближённое значение интеграла. Получаем при этом такую квадратурную формулу:
за приближённое значение интеграла. Получаем при этом такую квадратурную формулу: 