‹-- Назад
Квадратурная формула центральных прямоугольников
Снова рассмотрим отрезки разбиения ![]() , где
, где ![]() и
и ![]() ,
, ![]() , и выберем в качестве точек разметки середины каждого из этих отрезков, то есть точки
, и выберем в качестве точек разметки середины каждого из этих отрезков, то есть точки
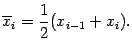
Получим тогда квадратурную формулу:
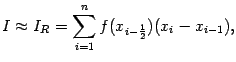
Если взять все отрезки разбиения равной длины ![]() , то эта квадратурная формула принимает вид
, то эта квадратурная формула принимает вид
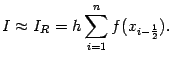
Для выяснения характера ошибки ![]() , возникающей при замене
, возникающей при замене ![]() на
на ![]() , заметим, что если функция
, заметим, что если функция ![]() дифференцируема, то прямоугольник площади
дифференцируема, то прямоугольник площади ![]() равновелик трапеции, верхней стороной которой служит касательная к графику
равновелик трапеции, верхней стороной которой служит касательная к графику ![]() , проведённая при
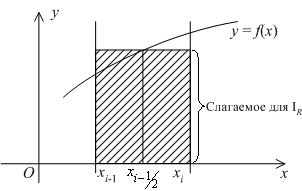
, проведённая при ![]() (см. рис.):
(см. рис.):
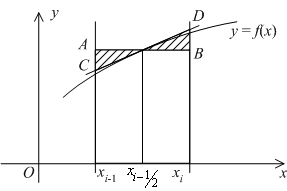
Действительно, заштрихованные на рисунке треугольники равны, отчего равны площади прямоугольника
Отсюда следует, что если функция ![]() имеет вторую производную, то при
имеет вторую производную, то при ![]() график является выпуклым кверху и
график является выпуклым кверху и ![]() (так как из чертежа видно, что площадь трепеции, равная
(так как из чертежа видно, что площадь трепеции, равная ![]() , больше площади под графиком функции, а при
, больше площади под графиком функции, а при ![]() график является выпуклым книзу и
график является выпуклым книзу и ![]() . Значит, при
. Значит, при ![]() на
на ![]() получаем
получаем ![]() , а при
, а при ![]() --
-- ![]() .
.