‹-- Назад

Основные обозначения и определения

Всюду в тексте учебника мы будем использовать общепринятые обозначения, те, что используются и в школьных учебниках. В частности,
означает числовую прямую (множество всех вещественных чисел);
означает множество натуральных чисел ;
означает множество всех целых чисел ;
означает пустое множество; по определению, в нём нет ни одного элемента;
, , и , где , , соответственно, -- замкнутые, полуоткрытые и открытые промежутки: квадратная скобка означает, что соответствующий конец промежутка включается в множество, а круглая скобка -- что не включается;
, , и , где ,  -- замкнутые и открытые лучи (бесконечные промежутки);
 -- числовая прямая, то же, что и ;
 -- пересечение (общая часть) множеств и ;
 -- объединение множеств и (все точки из и все точки из );
 -- множество тех элементов из , которые не принадлежат ;
 -- включение в ( -- это часть );
 -- принадлежность элемента множеству ( принадлежит );
 -- элемент не принадлежит множеству ;
 -- множество, состоящее из элементов ; в частности,  -- множество из одного элемента ;
 -- множество всех тех элементов из , для которых выполняется свойство .

        Определение 1.1   Пусть и  -- два произвольных множества. Функцией из в называется соответствие между элементами множества и множества , при котором каждому элементу сопоставляется какой-либо один элемент . При этом называется значением функции на элементе , что записывается как или . Тот факт, что функция переводит элементы в элементы , записывается так: . Множество называется областью определения функции и обозначается .     

Рис.1.1.Множество отображается функцией в множество


        Пример 1.1   Пусть в группе 20 студентов. Рассмотрим множество номеров и множество  -- множество фамилий, записанных русским алфавитом. Тогда соответствие , сопоставляющее каждому из номеров студентов в списке группы фамилию этого студента, -- это функция , где  -- номер студента в группе (от 1 до 20) и  -- фамилия этого студента. Поскольку фамилию имеет каждый студент, значение определено для всех . Очевидно, однако, что далеко не все элементы множества  -- множества всевозможных фамилий -- присутствуют в списке группы. Например, если в группе нет студента по фамилии Иванов, то элемент Иванов  не будет значением ни при каком . Если же в группе есть однофамильцы по фамилии Петров, то при разных номерах и элемент Петров  будет значением функции , то есть и .    

На этом примере видно, что, во-первых, множество значений функции

не обязано совпадать со всем множеством , а может оказаться лишь его частью. Во-вторых, могут найтись такие , что , но . В таком случае часто говорят, что элементы и склеиваются при отображении .

        Определение 1.2   Если , то есть для любого элемента найдётся элемент такой, что , то функция называется отображением на (напомним, что в общем случае  -- это отображение из в ). Отображение "на" также называют сюръективным отображением или сюръекцией.

Если для любых двух разных элементов ( ) значения тоже разные ( ), то отображение называется вложением множества в множество , или инъективным отображением (инъекцией).     

        Пример 1.2   Пусть и отображение для задано формулой . Тогда  -- сюръекция, так как любое число из отрезка равно значению при некотором .     

Рис.1.2.Все числа  -- это значения функции


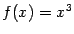
        Пример 1.3   Пусть и отображение задано при формулой . Тогда отображение одновременно является и сюръекцией, и инъекцией, так как
1) любое значение есть значение при некотором (а именно, при );
2) никакие два разных значения не могут дать одинаковых значений , так как из неравенства следует неравенство .    

Рис.1.3.Кубы разных чисел не совпадают


        Определение 1.3   Отображение , которое одновременно является и сюръекцией, и инъекцией, называется взаимно-однозначным соответствием между и , или биекцией. Это означает, что каждому элементу сопоставляется ровно один элемент , причём для каждого элемента имеется такой элемент , который сопоставлен этому .     

        Замечание 1.1   Если отображение  -- вложение, то мы можем рассмотреть соответствие, которое устанавливает эта функция между элементами множества и множеством значений функции , то есть частью множества . Пусть . Тогда функция устанавливает взаимно-однозначное соответствие между множествами и . (Более формально: функция , совпадающая с при всех , -- это биекция. 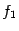В таких ситуациях, когда функции и имеют одну и ту же область определения и их значения совпадают при всех , мы в дальнейшем будем их обозначать одинаково, в данном случае -- буквой .)     

Рис.1.4.Множество взаимно-однозначно отображается на множество


        Пример 1.4   При сдаче пальто в гардероб каждому сданному пальто соответствует ровно один выданный номерок . Таким образом, между множеством сданных пальто и множеством выданных номерков ( -- это подмножество множества всех номерков в гардеробе) устанавливается биекция (, ).     

        Определение 1.4   Если  -- биекция, то отображение, сопоставляющее каждому тот элемент , который переходит в этот самый при отображении , называется обратным отображением (или обратной функцией) к отображению и обозначается . Таким образом, , и тогда и только тогда, когда (, ).     

        Пример 1.5   В условиях примера 1.4 отображение  -- биекция. При выдаче пальто из гардероба по каждому из выданных номерков находят соответствующее номерку пальто . Соответствие , (, ) -- это обратная функция к функции , , то есть .     

Очевидно, что в случае, если  -- биекция и  -- обратная к функция, то для всех и для всех . Последнее равенство показывает, что и что функции и взаимно обратны. (То есть если 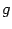 -- функция, обратная к , то  -- функция, обратная к .)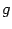

Рис.1.5.Функции и взаимно обратны


Итак, для того чтобы функция имела обратную функцию , функция должна быть биекцией, то есть устанавливать взаимно-однозначное соответствие между и . Тогда обратная функция устанавливает взаимно-однозначное соответствие между и .

        Пример 1.6   Функция , заданная формулой , -- это биекция. Обратная к ней функция -- это квадратный корень: .     

Рис.1.6.Функции 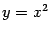и  -- взаимно обратны


В математическом анализе основную роль играют такие функции , у которых значениями служат вещественные числа, то есть . Такие функции называются числовыми. Функции примеров 1.2, 1.3, 1.6 -- числовые. Функции примеров 1.1, 1.4 числовыми не являются.

А вот пример числовой функции, область определения которой, в отличие от предыдущих примеров числовых функций, не лежит на числовой прямой.

        Пример 1.7   Пусть  -- множество всевозможных отрезков , расположенных в (трёхмерном) пространстве, концы которых (точки и ) не совпадают. Пусть соответствие сопоставляет каждому такому отрезку его длину . Так как длина отрезка -- число, то  -- числовая функция, . Легко видеть, что область её значений состоит из всех положительных чисел: .     

        Замечание 1.2   В первых главах учебника мы ограничимся в основном такими числовыми функциями , область определения которых также является подмножеством числовой прямой , то есть такими функциями , где и . Такие функции называются числовыми функциями одного переменного. В дальнейшем (во втором семестре) мы будем также изучать функции, зависящие от нескольких вещественных переменных, то есть функции, область определения которых -- подмножество в пространстве , равном прямому произведению экземпляров множества (определение прямого произведения нескольких множеств мы дадим ниже).     

        Определение 1.5   Графиком функции называется множество пар элементов и , такое, что в каждой паре второй элемент  -- это значение функции , соответствующее первому элементу пары, то есть .

Рассмотрим множество всевозможных пар , где , . Это множество всевозможных пар называется прямым произведением множества на множество и обозначается .     

Ясно, что график функции  -- это подмножество прямого произведения :

В некоторых из рассмотренных выше примеров функций были приведены на рисунках графики этих функций. График примера 1.2 -- подмножество в ; график примера 1.3 -- подмножество в ; оба графика примера 1.6 -- подмножества в (здесь мы ввели обозначение , которого будем придерживаться и далее).

        Пример 1.8   Пусть  -- круг радиуса 1 (включая окружность радиуса 1 -- границу круга) на числовой плоскости с координатами и , с центром в точке . Функцию в любой точке круга зададим как расстояние от этой точки до центра. Таким образом, , где .

Графиком этой функции является подмножество прямого произведения . Это прямое произведение -- бесконечный цилиндр с круговым сечением, находящийся в пространстве . Обозначим координаты точек в через . Тогда графику принадлежат те точки, для которых выполнены соотношения и .

Множество представляет собой кусок конической поверхности с вершиной в точке , с высотой 1 и радиусом основания 1.     


Рис.1.7.График расстояния до точки  -- это конус


Как мы видим, в случае, когда  -- подмножество плоскости , график числовой функции  -- это подмножество точек пространства . Если же  -- подмножество точек пространства , то графиком числовой функции будет подмножество четырёхмерного пространства, точнее, его подмножества . В связи с этим, изобразить график такой функции на чертеже не представляется возможным, хотя, конечно, можно постараться как-то этот график описать каким-то иным способом.

        Пример 1.9   Пусть и для каждой точки значение функции в этой точке -- это квадрат расстояния от до точки , то есть . Тогда график  -- это подмножество в :

Изобразить этот график, то есть нарисовать трёхмерную поверхность, расположенную в четырёхмерном пространстве, мы уже не в состоянии, однако формула позволяет изучать этот график. Например, можно заметить, что двумерное сечение этого графика плоскостью  -- это парабола в плоскости , а сечение трёхмерным пространством  -- это одна точка .    

Наибольший интерес с точки зрения наглядности представляют графики числовых функций одного переменного. Изучению поведения таких функций и построению их графиков будет уделено основное внимание в следующих главах.

Как мы видим из приведённых выше примеров, способы эти могут быть самые разные, от словесно-описательного в примерах 1.1, 1.4 до задания функции формулой вида в примерах 1.2, 1.3, 1.6, 1.8, 1.9. Способ задания функции зависит от того, какова природа множеств и и как по заданному определяется . Выделим основные из этих способов.





Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции

на главную
Hosted by uCoz