‹-- Назад
Открытые и замкнутые области в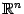 
с вешественными значениями, область определения которой 
-- подмножество 
-мерного пространства , 
. Таким образом,
--
, то есть числа 
( 
) -- те переменные, от которых зависит значение 
функции . Нас будут интересовать функции, областями определения которых служат открытые или замкнутые подобласти 
в . Дадим определение того, что такое открытая и замкнутая области.
множества 
назовём внутренней точкой , если входит в вместе с некоторой своей шаровой окрестностью:
обозначен радиус шаровой окрестности 
; в качестве расстояния 
мы будем брать декартово расстояние между точками, так что расстояние между точками 
и 
равняется 
.) 
Множество всех внутренних точек множества
называется внутренностью множества и обозначается 
. Множество называется открытым, если все его точки -- внутренние, то есть если оно совпадает со своей внутренностью: 
. Открытое множество в часто называют также открытой областью.
являются открытыми областями: 1) всё пространство
; 2) шар
радиуса 
с центром в начале координат; его точки -- те точки пространства, которые удовлетворяют неравенству 
; 3) полупространство, заданное соотношением
, где 
-- некоторые фиксированные числа (ограничивающая это полупространство гиперплоскость 
в полупространство не включается); 4) положительный октант
. Проверьте, что все эти множества открыты.
Легко видеть, что верно следующее утверждение.
. Тогда их объединение 
также является открытым множеством.
Пусть задан конечный набор открытых множеств 
. Тогда их пересечение 
также является открытым множеством.
Докажите эту теорему в качестве упражнения, исходя из определения открытого множества. Приведённый здесь рисунок используйте как подсказку к доказательству теоремы.
назовём граничной точкой множества , если её шаровая окрестность 
произвольного, как угодно малого, радиуса 
содержит как точки множества , так и точки, не принадлежащие . 
Совокупность всех граничных точек множества
называется границей множества и обозначается 
.
, очевидно, не имеет ни одной граничной точки, так что 
. 2) Границей шара радиуса служит сфера того же радиуса с тем же центром: 
3) Границей полупространства служит гиперплоскость , его определяющая.
называется замкнутым, если все граничные точки этого множества ему принадлежат, то есть если 
. Назовём дополнением в к множеству множество всех тех точек 
, которые не принадлежат , то есть множество
для любого множества . Имеет место следующее утверждение:
замкнуто тогда и только тогда, когда его дополнение 
открыто, и наоборот, множество открыто тогда и только тогда, когда его дополнение замкнуто. Докажите это утверждение в качестве упражнения. Из него и теоремы 7.1 сразу вытекает следующая теорема, если перейти к дополнениям:
. Тогда их пересечение также является замкнутым множеством. Пусть задан конечный набор замкнутых множеств . Тогда их объединение также является замкнутым множеством.
Докажите это утверждение в качестве упражнения, следуя указанию, данному перед формулировкой теоремы.
Из любого множества можно получить замкнутое множество, если присоединить к все его граничние точки, то есть рассмотреть множество 
. Множество 
называется замыканием множества .
Множество называется замкнутой областью, если оно является замыканием некоторой открытой области (своей внутренности), то есть если 
является замкнутой областью, так как его граница пуста. Замыканием открытого шара 
служит замкнутый шар 
, получающийся добавлением к открытому шару сферы 
. Замкнутый шар является замкнутой областью.
Замыканием открытого полупространства 
служит замкнутое полупространство 
, полученное добавлением к открытому полупространству ограничивающей его гиперплоскости 
. Замкнутое полупространство является замкнутой областью.
Замыканием положительного октанта служит неотрицательный октант
Однако не любое замкнутое множество в является замкнутой областью. Например, гиперплоскость 
содержит все свои граничные точки (она вся состоит из своих граничных точек) и, следовательно, замкнута. Однако внутренних точек она не имеет (никакой шар не лежит целиком в гиперплоскости). Поэтому её внутренность 
, и замыкание внутренности также пусто, то есть не совпадает с . Значит, не является замкнутой областью, поскольку 
.
замкнуто, то 
.
и 
-- график функции , на отрезке 
, рассматриваемый как подмножество двумерного пространства -- плоскости 
. Докажите, что 
не может являться открытым множеством. Пусть теперь функция имеет областью определения отрезок . Докажите, что её график является замкнутым подмножеством плоскости 
тогда и только тогда, когда функция непрерывна на 
.
график функции 
, при 
. Докажите, что -- не замкнутое множество и что 
, где 
-- отрезок 
на оси 
.
, . Рассмотрим интервалы 
и отрезки 
и их прямые произведения:
-- открытая область в и что 
-- её замыкание (то есть замкнутая область). Множество будем называть открытым брусом, или открытым параллелепипедом, а множество -- замкнутым брусом, или замкнутым параллелепипедом.
