‹-- Назад
Связные множества
Введём ещё несколько понятий, относящихся к множествам точек вПусть ![]() -- отрезок
-- отрезок ![]() на вещественной оси
на вещественной оси ![]() , переменная на которой обозначается буквой
, переменная на которой обозначается буквой ![]() . Рассмотрим
. Рассмотрим ![]() функций
функций ![]() , заданных на отрезке
, заданных на отрезке ![]() . Каждому
. Каждому ![]() соответствует тогда точка
соответствует тогда точка ![]() пространства
пространства ![]() . Получаем отображение
. Получаем отображение
Пусть теперь все функции ![]() , задающие вектор-функцию
, задающие вектор-функцию ![]() , непрерывны на отрезке
, непрерывны на отрезке ![]() . Тогда и вектор-функцию
. Тогда и вектор-функцию ![]() будем называть непрерывной. Для такой непрерывной вектор-функции, при изменении
будем называть непрерывной. Для такой непрерывной вектор-функции, при изменении ![]() на отрезке
на отрезке ![]() точка
точка ![]() непрерывно перемещается из положения
непрерывно перемещается из положения ![]() в положение
в положение ![]() .
.
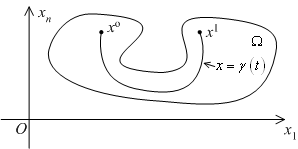
Множество всех точек
Заметим, что одна и та же линия ![]() может иметь разные параметризации. Например, на плоскости
может иметь разные параметризации. Например, на плоскости ![]() с координатами
с координатами ![]() отрезок
отрезок ![]() оси
оси ![]() можно параметризовать, положив либо
можно параметризовать, положив либо ![]() , либо
, либо ![]() (разумеется, формулы
(разумеется, формулы ![]() , при любом
, при любом ![]() задают ещё бесконечное множество различных параметризации той же линии
задают ещё бесконечное множество различных параметризации той же линии ![]() ).
).
На следующем рисунке приведены примеры связных областей на плоскости.
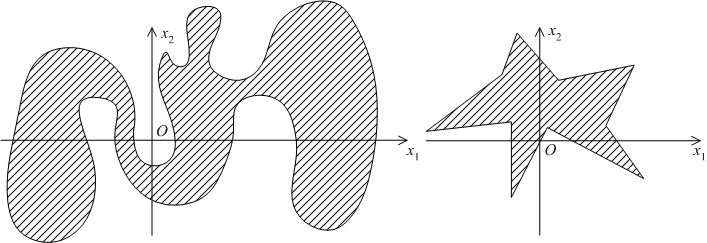
Связными областями являются:
1) всё пространство
2) замкнутые и открытые шары;
3) гиперплоскости;
4) замкнутые и открытые полупространства;
5) замкнутые и открытые параллелепипеды;
6) положительный и неотрицательный октанты.
Получаем, что, во-первых, все перечисленные выше в пунктах 1) -- 6) множества являются выпуклыми и что, во-вторых, любое выпуклое множество связно.
Более подробно выпуклые множества мы будем изучать ниже.
Приведём пример несвязной области.
Если взять две точки ![]() и
и ![]() , такие что
, такие что ![]() и
и ![]() , то обе они принадлежат
, то обе они принадлежат ![]() , поскольку их первая координата отлична от 0. Предположим, что некоторый непрерывный путь
, поскольку их первая координата отлична от 0. Предположим, что некоторый непрерывный путь ![]() соединяет точку
соединяет точку ![]() с точкой
с точкой ![]() и
и ![]() .
.
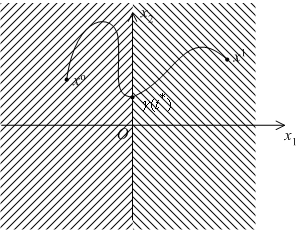
Поскольку
Если фиксировать некоторую точку ![]() множества
множества ![]() и рассмотреть все те точки
и рассмотреть все те точки ![]() , в которые ведут непрерывные и целиком лежащие в
, в которые ведут непрерывные и целиком лежащие в ![]() пути, выходящие из
пути, выходящие из ![]() , то множество таких концевых точек
, то множество таких концевых точек ![]() образует компоненту связности множества
образует компоненту связности множества ![]() , содержащую точку
, содержащую точку ![]() . Если эта компонента связности не охватывает всё множество
. Если эта компонента связности не охватывает всё множество ![]() , то можно рассмотреть какую-то точку
, то можно рассмотреть какую-то точку ![]() , не лежащую в этой компоненте, и, начиная с этой точки
, не лежащую в этой компоненте, и, начиная с этой точки ![]() , построить другую компоненту связности множества
, построить другую компоненту связности множества ![]() , не пересекающуюся с первой компонентой связности. Продолжая, если нужно, этот процесс далее, мы получаем разбиение множества
, не пересекающуюся с первой компонентой связности. Продолжая, если нужно, этот процесс далее, мы получаем разбиение множества ![]() на непересекающиеся компоненты связности.
на непересекающиеся компоненты связности.
Любое связное множество состоит из одной компоненты связности, а любое несвязное множество -- по меньшей мере из двух компонент связности.