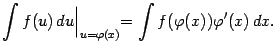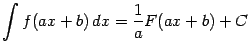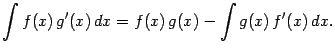‹-- Назад
Свойства неопределённого интеграла
Свойства первообразных и неопределённого интеграла вытекают из определения и соответствующих свойств производных.
1. Из определения вытекает, что
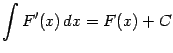
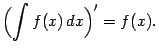
2. Имеет место равенство:
-- произвольная постоянная. Для доказательства обозначим через 
некоторую первообразную для 
, а через 
-- некоторую первообразную для 
. Тогда равенство означает, что 
, где 
-- постоянная. Это равенство верно, поскольку производные левой и правой частей дают одно и то же: 
, так как -- первообразная для , а 
, так как постоянный множитель можно вынести за знак производной и 
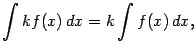
. Итак, постоянный множитель можно вынесить за знак интеграла.
3. Интеграл от суммы равен сумме интегралов:
равна , для 
равна , а для 
равна 
. Тогда равенство означает, что
. Поскольку
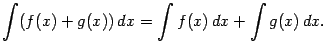
Свойства 2 и 3 называются свойствами линейности неопределённого интеграла. Из них следует, что для любых постоянных 
и 
, пользуясь линейностью интеграла. Этот интеграл можно разбить на два интеграла, от каждого из слагаемых, и вынести в обоих постоянные множители за знак интеграла:  | |
 |
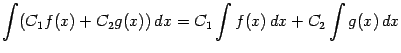
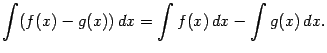
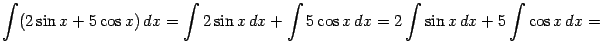Заметим, что произвольное постоянное слагаемое достаточно записать один раз: написав
и 
, мы сгруппировали бы постоянные слагаемые и получили произвольную постоянную 
.
4. Формула замены переменного. Пусть имеет смысл сложная функция 
, где 
изменяется на некотором интервале. Тогда
(В левой части после вычисления интеграла
сделана подстановка 
.) Для доказательства обозначим через 
некоторую первообразную для 
и через -- первообразную для 
. Это означает, что 
и 
. Доказываемое равенство (1.3) эквивалентно тогда такому:
. Формула (1.3) доказана. Заметим, что выражение 
в правой части (1.3) есть не что иное, как дифференциал 
функции . Так что мы можем записать (1.3) в виде
в обозначении неопределённого интеграла как некоторый дифференциал, а не просто как элемент обозначения интеграла, вроде скобки.
. Возьмём 
, тогда 
и 
. Подставляя это выражение под знак интеграла, получаем:
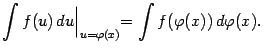
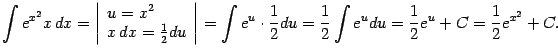
Всюду, где выражение зависит от 
, имеется в виду подстановка 
; освободившись от интеграла, мы выполняем эту подстановку в явном виде.
Линейная замена. Разберём особо случай, когда подынтегральная функция зависит от линейного выражения 
(где 
), то есть интеграл имеет вид
, откуда 
и 
. Пусть известна первообразная 
для 
:
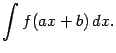
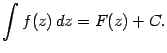
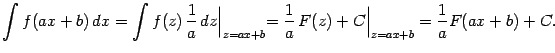
Полученную формулу
мы будем далее широко использовать, не всегда делая ссылки на её номер (1.4). Эту формулу следует хорошо запомнить, в особенности то, что при интегрировании с помощью линейной замены вперёд выходит множитель
, а не 
, как при дифференцировании функции 
. Например,
получаем
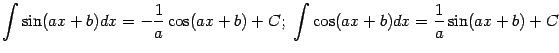
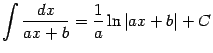
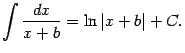
5. Формула интегрирования по частям. Пусть функции и имеют производную на рассматриваемом интервале изменения . Тогда верно равенство
Эта формула называется формулой интегрирования по частям. Она позволяет "перебрасывать" производную с функции
, стоящей под знаком интеграла, на другой подынтегральный множитель . При этом в правой части равенства появляется внеинтегральный член 
. Пусть -- первообразная для 
и -- первообразная для 
. Тогда равенство (1.5) можно записать в виде
-- некоторая постоянная. Докажем, что производные левой и правой частей совпадают. По определению, 
. С другой стороны,
Вводя обозначения 
и 
и замечая, что 
и 
, мы можем записать формулу интегрирования по частям в виде
, применив формулу интегрирования по частям. Положим 
и 
. Тогда 
и 
. Значит,
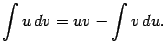
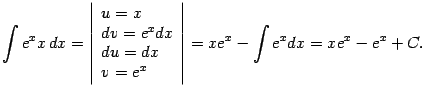
Здесь интеграл, получившийся в правой части при применении интегрирования по частям, является табличным, то есть он оказался проще исходного, что и привело нас к успеху в вычислении.
мы переходим к функции 
под знаком интеграла в правой части (точнее, к дифференциалу ), то есть функцию мы дифференцируем. Одновременно от функции 
(или от дифференциала ) мы переходим под интегралом в правой части к , то есть функцию 
мы интегрируем (напомним, что первообразная для 
есть ). Таким образом, применять формулу интегрирования по частям для вычисления неопределённого интеграла разумно в двух случаях:
а) либо когда функция "не слишком ухудшается" при дифференцировании, а функция "значительно улучшается" при интегрировании;
б) либо когда функция "значительно улучшается" при дифференцировании, а функция "не слишком ухудшается" при интегрировании.
Тогда дело в целом оправдано: происходит "некоторое улучшение" интеграла в правой части по сравнению с интегралом в левой части, в том смысле, что интеграл в правой части оказывается проще исходного.
В разобранном выше примере мы дифференцировали функцию 
, от чего она "сильно улучшилась": 
. Функцию 
мы интегрировали, отчего она "не сильно ухудшилась" (точнее говоря, совсем не изменилась, поскольку 
). В результате интеграл в правой части оказался проще исходного.
Приведём ещё один пример, подкрепляющий эти эмпирические соображения:
. Здесь разбить подынтегральное выражение 
на два множителя и 
можно только так: 
и 
. При этом дифференцирование приводит к упрощению (то есть к "улучшению", с точки зрения вычисления интеграла): 
, при этом "исчез" логарифм, который можно считать более сложной функцией, чем степень . Интегрирование же множителя даёт , то есть не сильно "ухудшает" этот множитель. Поэтому оправдано применение интегрирования по частям:
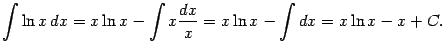
Дадим советы по наиболее часто встречающимся случаям применения этой формулы.
Если в подынтегральной функции содержатся как множители степень 
(где 
) и синус, косинус или экспонента (показательная функция), то имеет смысл взять 
и дифференцировать, а к отнести синус, косинус или экспоненту, умноженные на , и интегрировать этот множитель. При этом степень при дифференцировании понизится, синус при интегрировании перейдёт в косинус, а косинус в синус (это не приведёт к сильному усложнению), экспонента же вовсе не изменится. В целом интеграл в правой части будет проще исходного.
Таким способом можно, например, вычислить интегралы 
, 
, 
и подобные им. Иной раз формулу интегрирования по частям приходится применять и к тому интегралу, что образовался в правой части после первого интегрирования по частям.
Если же в подынтегральном выражении имеется степенная функция 
и одна из функций 
или 
, то к дифференциалу лучше отнести , а дифференцировать множитель, содержащий одну из перечисленных функций. Так мы и поступили в рассмотренном выше примере 1.7. Дело в том, что степенная функция при интегрировании остаётся степенной функцией, лишь показатель степени повышается на 1, а перечисленные функции при дифференцировании "улучшаются" (см. таблицу производных). По этому способу можно вычислить, например, интегралы 
, 
, 
, 
.
Указание. В первом из интегралов после применения формулы интегрирования по частям сделайте замену 
в образовавшемся в правой части интеграле.
При вычислении второго интеграла после интегрирования по частям получится интеграл 
. Его можно вычислить, применив снова формулу интегрирования по частям; при этом в правой части получается такой же интеграл 
, после чего находим из образовавшегося уравнения:
 | |
 | |
 |
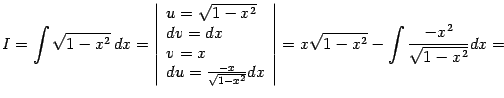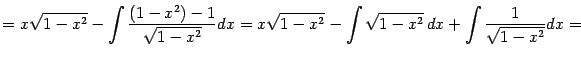Получаем уравнение
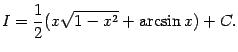
После интегрирования по частям в третьем интеграле в правой части получается интеграл 
. Преобразуйте его к виду 
(при каком предположении такое преобразование можно сделать?) и сделайте замену 
.
Наконец, для вычисления четвёртого интеграла примените формулу интегрирования по частям последовательно два раза.
Ниже мы разберём вычисление этих интегралов подробнее.
