mathserfer.narod.ru

Теория по высшей математике

Второй способ задания функции: с помощью формулы

Если множество бесконечно, то способ перечисления значений уже не годится. В этом случае функция может быть задана некоторой формулой, позволяющей по каждому значению аргумента найти соответствующее ему значение , например:

		при
		при
		при
		при

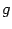
        Замечание 1.3   Функции, заданные одной и той же формулой, но на разных множествах , считаются различными. Так, функция при и функция при  -- это две разные функции, так как функция устанавливает соответствие между точками множества и некоторыми точками числовой прямой, а функция  -- между точками другого множества и точками числовой прямой. Конечно, две эти функции -- "близкие родственники", так как при всех .     

        Определение 1.6   Если дана функция , и , то мы можем получить новую функцию, рассматривая значения функции только на элементах . Эта функция определена равенством при . Функция называется ограничением функции на подмножество её области определения и обозначается , то есть .     

        Пример 1.12   Пусть  -- числовая плоскость и функция  задана формулой

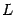
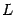
Рассмотрим на плоскости подмножество -- прямую линию , заданную уравнением . Тогда мы можем рассмотреть в качестве аргументов функции точки только прямой . Ограничение определено только при , поэтому его, кроме исходной формулы

можно задать такими формулами:

(1.1)

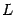
(так как на прямой ), или

(1.2)

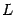
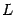
(так как на прямой ). Во всех точках прямой все три формулы дают одно и то же значение функции . Мы видим, что формула (1.1) даёт для те же значения, что функция одного переменного : , а формула (1.2) -- те же значения, что функция одного переменного : .

Две последние функции называются параметризациями ограничения .     

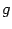
        Пример 1.13   Пусть  -- функция, заданная во всех точках плоскости . Пусть  -- прямая на плоскости . Тогда функция равна . Формально ограничение зависит от точек плоскости , но только таких, что . Поэтому задание этого ограничения эквивалентно заданию числовой функции одного переменного . Функция  -- это одна из возможных параметризаций функции .     

        Замечание 1.4   Во многих учебных примерах при задании функции при помощи формулы не указывают область определения . При этом по умолчанию предполагается, что область определения  -- максимально допустимая, то есть она состоит из всех таких значений аргумента , для которых задающее функцию выражение имеет смысл. При этом могут возникнуть трудности с выяснением того, какова же именно область , если в этом возникнет необходимость.     

        Пример 1.14   Пусть функция задана формулой

По умолчанию считается, что области принадлежат все те точки , что . Разумеется, для каждой заданной точки проверить это условие несложно, однако описать множество в виде объединения промежутков числовой оси мы не сможем ввиду того, что затрудняемся решить "в явном виде" данное неравенство.     

Если  -- это множество натуральных чисел , то функция называется последовательностью. Так как содержит бесконечное множество чисел , то задать в виде таблицы значений , где , вообще говоря, нельзя. Однако если функция легко угадывается по своим значениям при небольших , её часто задают, выписывая таблицу нескольких первых значений.

        Пример 1.15   Пусть . Тогда, скорее всего, имеется в виду, что при любом . Эта формула не противоречит выписанным значениям и очень проста. По-видимому, именно её и имели в виду при выписывании первых членов последовательности. Однако можно подобрать и другие формулы, то есть указать другие функции, для которых получаются те же первые значения , но, быть может, другие значения .     

        Упражнение 1.1   Придумайте другую формулу, дающую те же самые значения , но при всех прочих ( ) дающую значения, не равные .

Указание: попробуйте, например, отыскать эту формулу в виде , подобрав коэффициенты так, чтобы формула была верна при . Получится система трёх линейных уравнений для трёх неизвестных , рещив которую, вы найдёте, что .     

В некоторых случаях члены последовательности, то есть значения для , удобно не задавать при помощи указания явной зависимости , а вычислять рекуррентно, то есть вычислять каждый последующий член по значениям нескольких предыдущих:

        Пример 1.16   Последовательность чисел Фибоначчи задаётся так: два первых члена полагают равными единице ( ), а при вычисляют по формуле . Таким образом, и т. д.¹     

        Упражнение 1.2   Подберите коэффициенты и в формуле

(1.3)

так, чтобы при и число было числом Фибоначчи. Докажите, что тогда формула (1.3) даёт значение , равное числу Фибоначчи и при всех .

Пусть (это один из корней уравнения , служащего характеристическим уравнением возвратной последовательности ). Покажите, что

при всех (формула Бине); выведите из этой формулы, что  -- это ближайшее к целое число.