‹-- Назад
Решение квадратных уравнений с вещественными коэффициентами
Вернемся к задаче, поставленной в начале главы: можно ли в поле комплексных чисел решить любое квадратное уравнение (пока только с вещественными коэффициентами)? Для квадратного уравнения
мы одно решение знаем: 
. Очевидно, что 
, поэтому 
. Следовательно, оба корня такого уравнения известны.
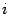
и 
в поле комплексных чисел абсолютно равноправны. Если бы число обозначить 
и построить с этим обозначением новое поле комплексных чисел, то оно будет в точности таким же, как и исходное. Рассмотрим уравнение 
, где 
-- вещественное положительное число. Легко проверить, что его корни 
, 
, где 
-- обычный арифметический корень.
Решим уравнение 
, где 
-- вещественные числа, 
, 
. Для этого выделим в правой части полный квадрат (см. пример 12.1):
обозначить 
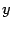
, а 
обозначить 
, то получим уравнение предыдущего типа, его решения:
отрицательный, то корни уравнения находятся по формулам: 
. Решение. Находим дискриминант:
Ответ: 
.
