‹-- Назад

Проекции вектора

Здесь и в дальнейшем под словами "проекция точки" или "проекция вектора" всегда будем понимать ортогональную проекцию.

Пусть в пространстве задана некоторая ось 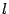, то есть прямая, на которой отмечена фиксированная точка 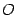и заданы направление и единица длины. Тогда каждой точке оси соответствует некоторое число.

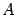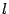
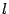
        Определение 10.21   Проекцией точки на ось называется число, соответствующее основанию перпендикуляра , опущенного на ось из точки .         

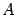
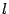
        Определение 10.22   Проекцией вектора на ось называется разность проекций конца вектора и его начала.         

Проекцию будем обозначать . На рис. 10.18 .




Рис.10.18.Проекция вектора на ось


Легко проверить, что если , то , то есть проекция не зависит от положения начала вектора, а зависит только от самого вектора.

        Предложение 10.13   Пусть  -- угол, образованный вектором a с осью . Тогда .

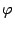
        Доказательство.     Пусть угол  -- острый. Тогда в соответствии с рис. 10.19 получим .




Рис.10.19.


Если угол 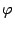тупой, то в соответствии с рис.10.20 находим ,




Рис.10.20.


откуда .    

        Предложение 10.14   Проекция на ось суммы векторов равна сумме их проекций.

        

Если проекции слагаемых одного знака, то доказательство очевидно из рис. 10.21.




Рис.10.21.Проекция суммы


Случай проекций разных знаков читатель может проанализировать самостоятельно или прочесть в одном из учебников из списка литературы.

        Предложение 10.15   Проекция на ось вектора, умноженного на число, равна произведению проекции вектора на это число.

        

Доказательство очевидно из подобия треугольников на рис. 10.22.




Рис.10.22.Проекция произведения вектора на число


        Определение 10.23   Проекцией вектора b на вектор a, , будем называть проекцию вектора b на любую ось, параллельную вектору a и имеющую направление, совпадающее с направлением вектора a.         

Проекция вектора b на вектор a обозначается .

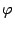Очевидно, что , где  -- угол между векторами a и b.

        Предложение 10.16   Проекции вектора на координатные оси равны коодинатам вектора.

        

        Определение 10.24   Косинусы углов, образованных вектором с осями координат, называются направляющими косинусами вектора.         




Рис.10.23.Направляющие косинусы вектора


В соответствии с рис. 10.23, направляющими косинусами вектора a являются , , .

        Предложение 10.17   Координаты вектора равны его направляющим косинусам, умноженным на длину вектора. Если вектор единичный, то его координатами служат направляющие косинусы.

        

Доказательство  предложений 10.16, 10.17 предоставляется в качестве упражнения читателю.



Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции

на главную
Hosted by uCoz