‹-- Назад
Вершины кривых
По аналогии с параболой мы можем дать такое определение:
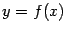
любую точку этой кривой, в которой кривизна 
имеет локальный экстремум. В соответствии с этим определением вершина параболы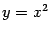 
является вершиной линии 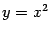в новом, обобщённом, смысле.
. Её верхняя половина (при 
) -- это график функции 
на отрезке 
. Возьмём точку 
и найдём кривизну окружности при этом 
. Имеем: 
. Поскольку 
, то кривизна прямой в любой точке равна 0. Как и у окружности, все точки прямой -- это её вершины. Заметим, что, по определению, кривизна неотрицательна, так что если она равна 0 в некоторой точке кривой 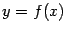, то эта точка является вершиной кривой. Поскольку 
это может случиться лишь при 
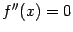, в частности, во всех точках перегиба функции 
(тех, где вторая производная существует).
. Поскольку вторая производная 
обращается в 0 при 
, то точка 
служит одной из вершин этой параболы: в ней кривизна принимает минимальное значение 0. 
имеет три вершины
Ответ: эти две вершины расположены при 
.
(
). Поскольку 
и 
, имеем 
. Рассмотрим часть гиперболы, лежащую при 
(вторая половина -- симметрична рассматриваемой). Поскольку 
-- возрастающая при 
функция, точки экстремума функций и
также возрастает при 
, достаточно сделать замену 
и перейти к нахождению экстремума функции 
имеет такой вид: 
Точка максимума 
ищется из условия 
; легко подсчитать, что
и 
-- абсцисса вершины гиперболы как кривой . С другой стороны, пересечение гиперболы с прямой находим из уравнения
. Отметим, что кривизна гиперболы в её вершине равна
на плоскости задаётся уравнением 
и 
-- положительные числа и 
. Покажите, что четыре точки пересечения эллипса с осями координат являются его вершинами, причём в двух вершинах кривизна принимает наибольшее значение, а в двух других -- наименьшее. Для этого рассмотрите, как из данного уравнения выражаются зависимости 
и 
.
Найдите значение кривизны в вершинах эллипса.
