‹-- Назад
Радиус кривизны
Определение 8.3 Радиусом кривизны кривой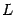 
в точке 
называется число 
, где 
-- кривизна линии в точке 
. Если кривизна в точке равна 0, то радиус кривизны формально полагаем равным 
.
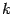в точке называется число , где -- кривизна линии 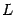в точке 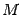. Если кривизна в точке 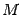равна 0, то радиус кривизны формально полагаем равным . Заметим, что для окружности это определение даёт значение радиуса кривизны, совпадающее с радиусом окружности (постоянное во всех точках окружности).
Без доказательства сообщим, что из всех окружностей, касающихся линии в фиксированной точке 
, наиболее плотно прилегает24 к линии та окружность, которая имеет радиус, равный радиусу кривизны кривой в точке , и выпуклость в ту же сторону, что кривая . Эта окружность называется окружностью кривизны линии в точке .
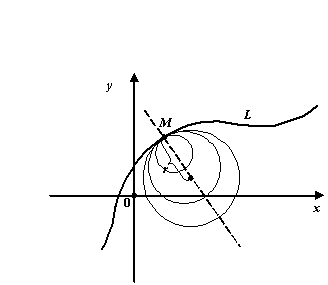
Рис.8.6.Окружности, касающиеся линии 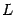, и окружность кривизны
, и окружность кривизны
Пример 8.7 Радиус кривизны параболы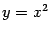 
в её вершине равен 
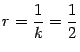. Значит, окружность радиуса 
с центром в точке 
наилучшим образом приближает параболу в окрестности её вершины, то есть является для параболы окружностью кривизны в вершине параболы.
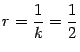в её вершине равен . Значит, окружность радиуса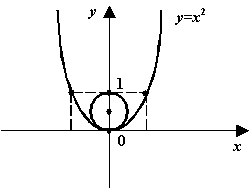 с центром в точке наилучшим образом приближает параболу в окрестности её вершины, то есть является для параболы окружностью кривизны в вершине параболы. 
Рис.8.7.Окружность кривизны для параболы в вершине
Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции
