mathserfer.narod.ru

Теория по высшей математике

‹-- Назад

Приведение уравнения второго порядка к каноническому виду

В главе "Поверхности второго порядка", где рассматривались поверхности второго порядка, было выписано их общее уравнение (13.1), а дальше для каждой поверхности использовалась своя прямоугольная декартова система координат, в которой уравнение поверхности имело канонический вид. В этом разделе мы выясним, как по общему уравнению найти такую систему координат. Результаты этого раздела используются и для приведения общего уравнения кривой второго порядка к каноническому виду. Достаточно будет во всех рассуждениях отбросить третью координату.

Пусть в пространстве задана прямоугольная декартова система координат . Рассмотрим общее уравнение поверхности второго порядка, коэффициенты в котором обозначены специальным образом

где  -- числа, причем хотя бы одно из чисел отлично от нуля.

Выделим квадратичную часть выражения, стоящего в уравнении слева,

Такое выражение называется квадратичной формой от трех переменных. Составим матрицу

Эта матрица называется матрицей квадратичной формы . Она является симметричной, то есть , или, другими словами, . Следует обратить внимание на то, как эта матрица составлена. На диагонали у нее стоят коэффициенты при квадратах переменных, а в остальных местах -- половины коэффициентов при произведениях переменных.

Исходная система координат является прямоугольной, поэтому скалярное произведение векторов с координатными столбцами , задается формулой . Сформулируем две теоремы, позволяющие пользоваться приведенным ниже алгоритмом.

Пусть -- матрица квадратичной формы . По сформулированной теореме у нее существует ортонормированный базис из собственных векторов. Обозначим их , , , и пусть эти векторы имеют координаты

Базис i, j, k назовем старым, а базис  -- новым. Тогда матрица перехода 19.1.4.а будет иметь вид

Выберем новую систему координат так, что начало координат не изменяется, а новые базисные векторы , , задают направления новых координатных осей , , (рис. 19.8).

Тогда координаты точки являются координатами ее радиус-вектора и, следовательно, при замене базиса меняются по формуле (18.1)

Если мы из равенства (19.8) выпишем выражение , , через новые переменные , , и подставим в уравнение (19.7), то обнаружим, что квадратичная его часть и линейная часть преобразуются независимо друг от друга. В результате уравнение в системе координат имеет вид

Хотя бы одно из чисел , , отлично от нуля, иначе матрица была бы нулевой.

Рассмотрим три случая.

1. Пусть все собственные числа 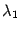, , отличны от нуля. В уравнении (19.9) выделим полные квадраты
   
   Выполним параллельный перенос системы координат , взяв за новое начало системы координат точку (см. формулы (13.21)). Тогда в новой системе координат уравнение запишется в виде
   
   Здесь возможны следующие варианты.
   1. Пусть . Перенесем в правую часть и поделим обе части на , получим
      
      1. Если числа , , отрицательны, то ни одна точка пространства не удовлетворяет этому уравнению. Говорят, что оно определяет мнимый эллипсоид.
      2. Если числа , , положительны, то уравнение является каноническим уравнением эллипсоида.
      3. Если одно из чисел , , отрицательно, а остальные положительны, то (после переименования осей) получим каноническое уравнение однополостного гиперболоида.
      4. Если одно из чисел , , положительно, остальные отрицательны, то (после переименования осей) получим каноническое уравнение двуполостного гиперболоида.
   2. Пусть .
      1. Если все числа , , положительны, то только начало координат удовлетворяет этому уравнению. Поверхность выродилась в точку.
      2. Если одно из чисел , , отрицательно, а два положительны, то (после переименования осей) получим каноническое уравнение конуса.
      Если же два числа отрицательны или все три отрицательны, то, умножив обе части уравнения на , получим случай 2 или случай 1.
2. Пусть одно из чисел 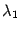, , равно нулю, а два других отличны от нуля. Допустим, что . Тогда в уравнении (19.9) выделим полные квадраты по переменным ,
   
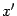   1. Пусть . Преобразуем уравнение к виду
      
      Поделим обе части уравнения на и выполним параллельный перенос осей координат, взяв за новое начало координат точку . Получим уравнение
      
      1. Если числа и положительны, то это -- каноническое уравнение эллиптического параболоида.
      2. Если , , получим каноническое уравнение гиперболического параболоида.
      Если числа и отрицательны или , , то сменим направление у оси 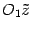на противоположное и получим либо случай 1, либо случай 2.
   2. Пусть . Тогда поверхность является цилиндрической, образующие которой параллельны оси , а направляющей служит кривая на плоскости с уравнением
      
      Анализ поверхностей с таким уравнением предоставляем читателю.
3. Пусть только одно из чисел 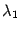, , отлично от нуля. Допустим, что . Тогда в уравнении (19.9) выделим полный квадрат по переменному
   
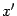
   1. Пусть хотя бы одно из чисел , отлично от нуля. Тогда на плоскости возьмем две перпендикулярные прямые и . Возьмем новую систему координат, у которой начало будет в точке 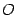, ось направлена по оси , ось направлена вдоль второй прямой, а ось направлена вдоль первой прямой. Тогда уравнение примет вид
      
      Это -- уравнение цилиндрической поверхности, образующие которой параллельны оси , а направляющей служит кривая на плоскости с уравнением
      
      Анализ возможных поверхностей оставляем читателю.
   2. Пусть . Тогда уравнение принимает вид
      
      1. Если число справа положительно, то уравнение определяет две плоскости
         

      2. Если число справа равно нулю, то уравнение определяет одну плоскость
         

      3. Если число справа отрицательно, то ни одна точка пространства уравнению не удовлетворяет.

Итак, получен алгоритм, позволяющий установить, какая поверхность задается уравнением второго порядка и каково ее положение в пространстве.

Подставим эти выражения в исходное уравнение. Квадратичная форма примет вид, в котором произведения переменных будут отсутствовать, а коэффициентами при квадратах будут служить собственные числа

Приводим подобные члены

Выделим полные квадраты

или

Выполняем параллельный перенос осей координат

Новое начало системы координат имеет координаты

В исходной системе координат точка в соответствии с формулами (19.10) имеет координаты

В новой системе координат (рис. 19.9) уравнение принимает канонический вид

Это уравнение является каноническим уравнением однополостного гиперболоида. Его центр находится в точке , две вещественные оси параллельны векторам , , вещественные полуоси равны , . Мнимая ось параллельна вектору , мнимая полуось равна . Изображение гиперболоида приведено на рисунке 19.10.