‹-- Назад
Метод одной касательной
Заметим, что в методе секущих удобно было бы фиксировать наиболее удобное для первого шага значение 
, при котором все секущие параллельны касательной, проведённой к графику 
при 
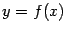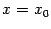. При таком выборе 
метод секущих называется методом одной касательной. Формула итераций этого метода имеет вид
или, что то же, 
. 
При таком выборе в точке 
выполнено равенство
, достаточно мал, а производная 
непрерывна, то значение 
будет не сильно отличаться от 
и, следовательно, график 
будет пересекать прямую 
, идя почти горизонтально. А это, как мы отмечали выше, будет давать нам быстрое приближение итераций к корню (так как число 
при этом можно выбрать равным 
, а эта величина мала).
. (Напомним, что его корень был ранее нами отделён на отрезке 
.) Корень будем находить с точностью до 
, а для этого вычисления будем вести до тех пор, пока в значении 
не зафиксируется шестой знак после десятичного разделителя. В качестве начального приближения возьмём 
. Поскольку
и 
. Значит, итерационная формула будет такой: 
 | |
 | |
 |
Восьмое и девятое приближения уже совпадают с точностью
, поэтому вычисления на этом прекращаем и полагаем 
.
, так что второй конец отрезка не годится для начального приближения метода одной касательной. Не забудьте, что значение зависит от начального приближения и потому изменится. Проверьте, сколько нужно итераций, чтобы найти то же значение корня, начав с 
и с 
.
Ответ: Потребуется и в том, и в другом случае 22 итерации.
