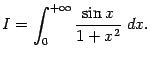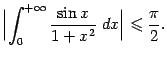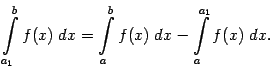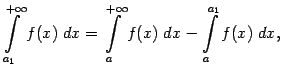‹-- Назад
Свойства несобственных интегралов первого рода
Напомним, что мы выяснили выше, что достаточно рассматривать только свойства интегралов вида 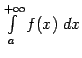 , а свойства интегралов вида
, а свойства интегралов вида 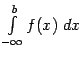 их будут повторять с очевидными исправлениями.
их будут повторять с очевидными исправлениями.
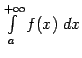 сходится, то при любом
сходится, то при любом 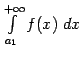 . Обратно, если при некотором
. Обратно, если при некотором 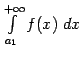 , то сходится и интеграл
, то сходится и интеграл 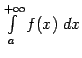 .
. Доказательство. Докажем, что из сходимости 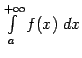 следует сходимость
следует сходимость 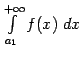 при
при ![]() . Из аддитивности интеграла следует, что при любом
. Из аддитивности интеграла следует, что при любом ![]() имеет место равенство
имеет место равенство
Переходя в этом равенстве к пределу при
причём несобственный интеграл в правой части сходится по условию теоремы, а интеграл
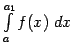 вовсе не зависит от
вовсе не зависит от 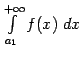 , существует (и равен
, существует (и равен 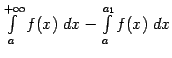 ), что доказывает сходимость интеграла
), что доказывает сходимость интеграла 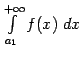 .
. Доказано на самом деле даже больше: кроме самомго факта сходимости интеграла 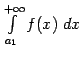 , мы доказали формулу (4.3).
, мы доказали формулу (4.3).
Из той же формулы (4.2) следует и второе утверждение теоремы. Действительно, по условию теоремы интеграл по конечному отрезку ![]() существует, поскольку функция интегрируема, так что при любом
существует, поскольку функция интегрируема, так что при любом ![]() из формулы (4.2) получаем:
из формулы (4.2) получаем:
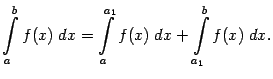 |
Отсюда переходом к пределу при
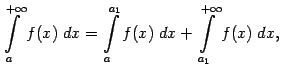 |
причём существование предела, задающего интеграл в левой части, следует из предположенной сходимости несобственного интеграла
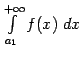 в правой части.
в правой части.
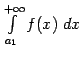 , а следовательно, и на факте сходимости (или, соответственно, расходимости) интеграла
, а следовательно, и на факте сходимости (или, соответственно, расходимости) интеграла 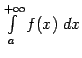 , хотя такое изменение может, конечно, привести к изменению значения этого интеграла.
, хотя такое изменение может, конечно, привести к изменению значения этого интеграла.
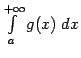 , следует сходимость интеграла от меньшей функции,
, следует сходимость интеграла от меньшей функции, 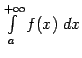 , причём
, причём а из расходимости интеграла от меньшей функции,
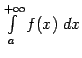 , следует расходимость интеграла от большей функции,
, следует расходимость интеграла от большей функции, 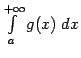 :
:
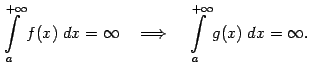
Доказательство. Поскольку ![]() , то функция
, то функция ![]() не убывает (геометрически значение функции равно площади криволинейной трапеции, лежащей над отрезком
не убывает (геометрически значение функции равно площади криволинейной трапеции, лежащей над отрезком ![]() , а эта площадь, очевидно, не убывает, если увеличивать
, а эта площадь, очевидно, не убывает, если увеличивать ![]() ). Точно так же не убывает и функция
). Точно так же не убывает и функция ![]() , причём по теореме об интегрировании неравенства получаем: из
, причём по теореме об интегрировании неравенства получаем: из ![]() следует, что
следует, что
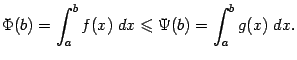
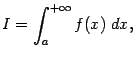
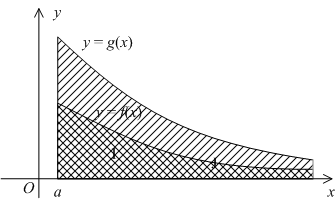
Геометрически доказанное утверждение почти очевидно: оно означает, что если площадь под верхним графиком на следующем рисунке (она заштрихована), конечна, то конечна и имеет меньшее значение площадь под нижним графиком (она имеет двойную штриховку).
Доказательство второго утверждения теоремы сразу следует из первого утверждения по принципу "от противного": предположим, что интеграл от меньшей функции расходится. Если бы утверждение было неверно и интеграл от большей функции оказался бы сходящимся, то вместе с ним сходился бы и интеграл от меньшей функции, вопреки предположению. Значит, второе утверждение теоремы верно.
Геометрически оно означает, что если площадь, обозначенная на рисунке двойной штриховкой, бесконечна, то, тем более, бесконечна и вся заштрихованная площадь.
Доказанная теорема означает, что сходимость несобственного интеграла -- это такое свойство, которое выполняется "тем лучше", чем меньше значения подынтегральной функции (однако, заметим, эти значения должны быть неотрицательными)!
Если условие неотрицательности функций ![]() и
и ![]() не предполагается, то оба утверждения теоремы могут оказаться не верны: так, если взять
не предполагается, то оба утверждения теоремы могут оказаться не верны: так, если взять ![]() и
и ![]() при всех
при всех ![]() , то интеграл от большей функции,
, то интеграл от большей функции,
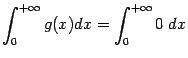
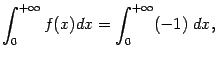 --
-- 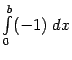 и рассмотрев его поведение при
и рассмотрев его поведение при Тот же пример показывает, что если функции не неотрицательны, то из расходимости интеграла от меньшей функции может не следовать расходимость интеграла от большей.
При помощи теоремы 4.2 мы можем в некоторых случаях исследовать сходимость интеграла, не вычисляя его значения. Для доказательства сходимости интеграла от функции ![]()
![]() достаточно найти более простую функцию
достаточно найти более простую функцию ![]() , для которой интеграл
, для которой интеграл ![]() легко вычисляется и сходится. Согласно теореме, тогда исходный интеграл тоже сходится, причём мы получаем оценку его величины:
легко вычисляется и сходится. Согласно теореме, тогда исходный интеграл тоже сходится, причём мы получаем оценку его величины: ![]() . Если же нам нужно доказать расходимость интеграла
. Если же нам нужно доказать расходимость интеграла ![]() , то достаточно найти такую (более просто устроенную) функцию
, то достаточно найти такую (более просто устроенную) функцию ![]() , что
, что ![]() и интеграл
и интеграл ![]() расходится.
расходится.
Приведём примеры, показывающие этот приём в действии и разъясняющие, как определять, что же для данного интеграла нужно доказывать: сходимость или расходимость10.
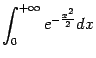
Для сравнения выберем функцию ![]() , неопределённый интеграл от которой легко считается:
, неопределённый интеграл от которой легко считается:
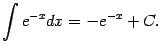
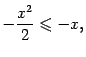
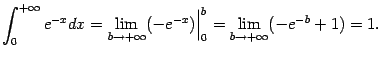
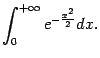
Для многих примеров при доказательстве сходимости или расходимости интеграла естественно сравнивать подынтегральную функцию с функцией вида ![]() . Определим, при каких значениях показателя
. Определим, при каких значениях показателя ![]() интеграл
интеграл
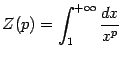
Рассмотрим случай ![]() . Тогда
. Тогда
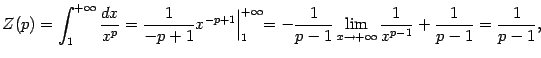
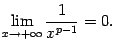
Рассмотрим случай ![]() . Тогда
. Тогда
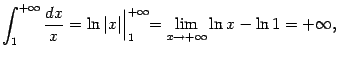
Рассмотрим случай ![]() . Тогда
. Тогда
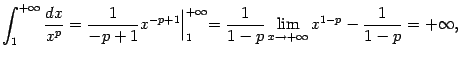
Итак, интеграл сходится (и функция ![]() определена и равна
определена и равна ![]() ) только при
) только при ![]() ; при
; при ![]() интеграл расходится.
интеграл расходится.
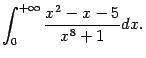
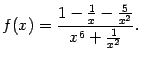
Интеграл от функции ![]() сходится: поскольку
сходится: поскольку ![]() , то получаем сходящийся интеграл
, то получаем сходящийся интеграл
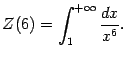
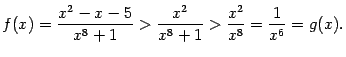
На основании теоремы 4.1 сходится и исходный интеграл.
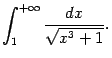
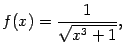
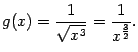
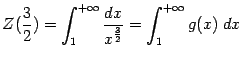
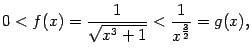
Итак, интеграл от большей функции ![]() сходится, откуда следует сходимость исходного интеграла
сходится, откуда следует сходимость исходного интеграла ![]()
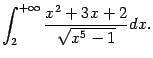
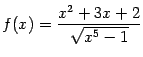
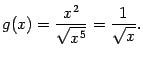
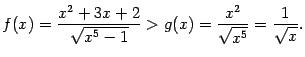
Итак, условия теоремы 4.2 проверены. На основании этой теоремы (точнее, её второго утверждения) мы можем заключить, что данный нам интеграл ![]() расходится.
расходится.
Докажем ещё одно важное свойство несобственного интеграла первого рода.
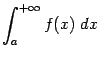
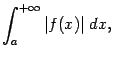
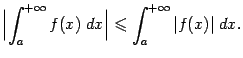
Доказательство. Представим ![]() в виде разности двух неотрицательных функций
в виде разности двух неотрицательных функций ![]() и
и ![]() :
:
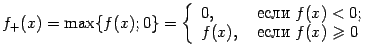
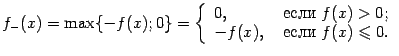
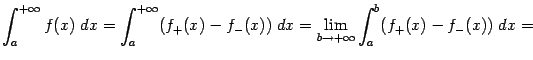 | |
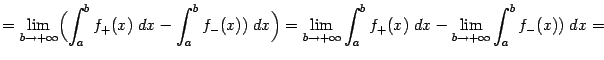 | |
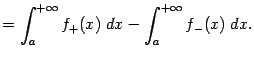 |
Мы доказали тем самым, что интеграл
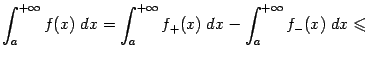 | |
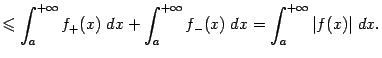 |
Но поскольку
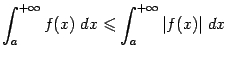 и
и 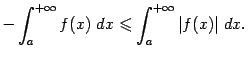
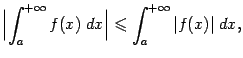
Если же несобственный интеграл ![]() расходится, а несобственный интеграл
расходится, а несобственный интеграл ![]() сходится, а несобственный интеграл
сходится, а несобственный интеграл ![]() называется условно сходящимся.
называется условно сходящимся.
Заметим, что доказанная только что теорема означает в точности, что любой абсолютно сходящийся интеграл сходится.
Доказательство. Поскольку ![]() и интеграл
и интеграл ![]() сходится, то по теореме 4.2 интеграл
сходится, то по теореме 4.2 интеграл ![]() также сходится. Это означает, что интеграл
также сходится. Это означает, что интеграл ![]() сходится абсолютно, откуда следует сходимость самого интеграла
сходится абсолютно, откуда следует сходимость самого интеграла ![]() , причём
, причём
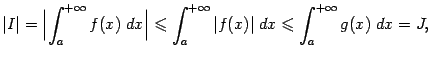
Таким образом, чтобы установить сходимость несобственного интеграла ![]() , достаточно найти для
, достаточно найти для ![]() на
на ![]() такую мажоранту
такую мажоранту ![]() , что интеграл
, что интеграл ![]() сходится.
сходится.