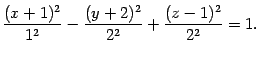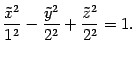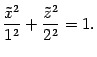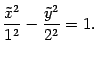‹-- Назад Так же как и на плоскости, в пространстве можно выполнить параллельный перенос системы координат. Формулы и их доказательства для пространственного случая аналогичны плоскому случаю (пункт 3.5).
Пусть в пространстве заданы две декартовы прямоугольные системы координат: "старая" с началом в точке 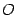 и осями
и осями 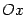 ,
, 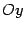 ,
, 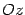 и "новая" с началом в точке
и "новая" с началом в точке 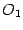 и осями
и осями 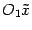 ,
, 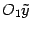 ,
, 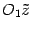 , причем оси одной системы координат соответствено параллельны осям другой системы и одинаково с ними направлены. Будем говорить, что вторая система координат получена из первой параллельным переносом.
, причем оси одной системы координат соответствено параллельны осям другой системы и одинаково с ними направлены. Будем говорить, что вторая система координат получена из первой параллельным переносом.
Пусть начало 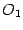 новой системы координат имеет в старой системе координаты
новой системы координат имеет в старой системе координаты 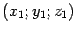 . Пусть
. Пусть 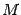 -- некоторая точка пространства с координатами
-- некоторая точка пространства с координатами 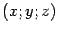 в старой системе координат и
в старой системе координат и 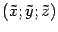 -- в новой системе координат. Тогда связь между "старыми" и "новыми" координатами точки
-- в новой системе координат. Тогда связь между "старыми" и "новыми" координатами точки 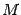 задается формулами, аналогичными формулам (12.11):
задается формулами, аналогичными формулам (12.11):
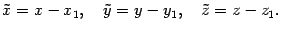 | (13.21) |
Справедливо и предложение, аналогичное предложению 12.7.
Пример 13.2 Нарисуйте поверхность
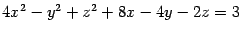
.
Решение. Выделим полные квадраты по переменным 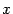 ,
, 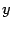 и
и 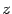 (см. пример 12.1):
(см. пример 12.1):
Отсюда
Разделим обе части на 4:
Введем новую систему координат с началом в точке
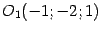
, получающуюся из старой параллельным переносом. По
предложению 13.1 получим, что в новой системе поверхность задается уравнением
Данное уравнение отличается от канонического уравнения однополостного гиперболоида тем, что поменялись ролями оси ординат (
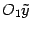
) и аппликат (
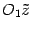
). Не переобозначая осей, произведем построение поверхности с помощью сечений. В сечении плоскостью
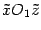
получаем эллипс с уравнением
Его полуоси равны 1 и 2 и лежат соответственно на осях
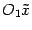
и
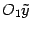
. В сечении плоскостью
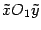
получаем гиперболу с уравнением
Ее мнимая ось лежит на оси
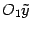
, а действительная ось лежит на оси
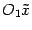
, полуоси соответственно равны 2 и 1. В сечении плоскостью
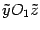
получаем равностороннюю гиперболу с уравнением
Ее мнимая ось лежит на оси
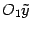
, а действительная ось лежит на оси
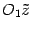
, обе полуоси равны 2. Для большей наглядности нарисуем еще два сечения плоскостями параллельными плоскости
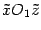
. В сечениях получим эллипсы, подобные эллипсу в плоскости
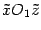
. По рассмотренным сечениям можно представить себе форму гиперболоида и его расположение в пространстве (рис. 13.33). Объемное изображение приведено на рис. 13.34.
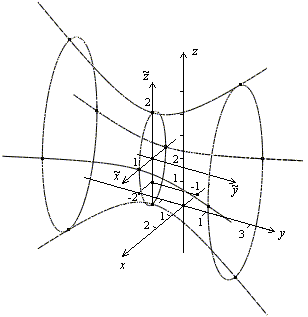
Рис.13.33.Изображение поверхности с помощью сечений
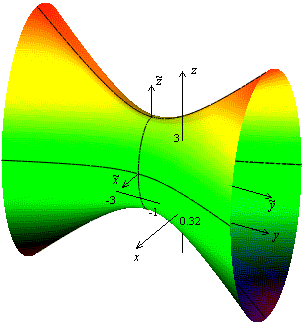
Рис.13.34.Объемное изображение поверхности
Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции
![]() и осями
и осями ![]() ,
, ![]() ,
, ![]() и "новая" с началом в точке
и "новая" с началом в точке ![]() и осями
и осями ![]() ,
, ![]() ,
, ![]() , причем оси одной системы координат соответствено параллельны осям другой системы и одинаково с ними направлены. Будем говорить, что вторая система координат получена из первой параллельным переносом.
, причем оси одной системы координат соответствено параллельны осям другой системы и одинаково с ними направлены. Будем говорить, что вторая система координат получена из первой параллельным переносом. ![]() новой системы координат имеет в старой системе координаты
новой системы координат имеет в старой системе координаты ![]() . Пусть
. Пусть ![]() -- некоторая точка пространства с координатами
-- некоторая точка пространства с координатами ![]() в старой системе координат и
в старой системе координат и ![]() -- в новой системе координат. Тогда связь между "старыми" и "новыми" координатами точки
-- в новой системе координат. Тогда связь между "старыми" и "новыми" координатами точки ![]() задается формулами, аналогичными формулам (12.11):
задается формулами, аналогичными формулам (12.11): ![]() ,
, ![]() и
и ![]() (см. пример 12.1):
(см. пример 12.1):