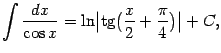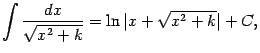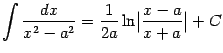‹-- Назад
Неопределённый интеграл и таблица неопределённых интегралов
Дадим теперь такое название множеству всех первообразных данной функции:
Согласно доказанным выше теоремам о виде первообразных, неопределённый интеграл от функции ![]() состоит из функций вида
состоит из функций вида ![]() , где
, где ![]() -- какая-либо фиксированная первообразная для
-- какая-либо фиксированная первообразная для ![]() , а
, а ![]() -- величина, постоянная на каждом из непересекающихся интервалов, на которых задана функция
-- величина, постоянная на каждом из непересекающихся интервалов, на которых задана функция ![]() . Поэтому можно написать такую формулу:
. Поэтому можно написать такую формулу:
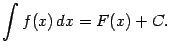
Итак, для того чтобы доказать равенство ![]() , достаточно проверить, что
, достаточно проверить, что ![]() -- первообразная для
-- первообразная для ![]() , то есть что
, то есть что ![]() . Поэтому таблица неопределённых интегралов для многих часто встречающихся функций сразу следует из таблицы производных, которую мы получили в первом семестре.
. Поэтому таблица неопределённых интегралов для многих часто встречающихся функций сразу следует из таблицы производных, которую мы получили в первом семестре.
1) Поскольку ![]() , то при
, то при ![]()
![]() и
и ![]() , если взять
, если взять ![]() . Поэтому при
. Поэтому при ![]()
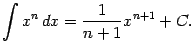
В частности, получаем при ![]() (заметим, что
(заметим, что ![]() ):
):
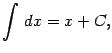
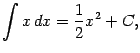
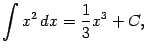
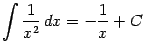
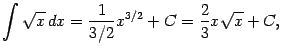
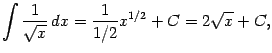
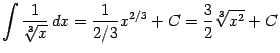
2) Пусть ![]() . Тогда
. Тогда ![]() не задаётся формулой предыдущего пункта. Однако, согласно таблице производных, при
не задаётся формулой предыдущего пункта. Однако, согласно таблице производных, при ![]() мы имеем
мы имеем ![]() , следовательно,
, следовательно, ![]() -- первообразная для
-- первообразная для ![]() на интервале
на интервале ![]() . Проверим, что при
. Проверим, что при ![]() функция
функция ![]() -- первообразная для
-- первообразная для ![]() на интервале
на интервале ![]() . Действительно, по правилу дифференцирования сложной функции получаем
. Действительно, по правилу дифференцирования сложной функции получаем
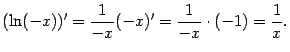
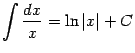
3) Поскольку, согласно таблице производных, при ![]()
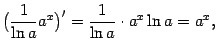
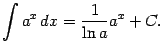
В частности, при ![]() получаем:
получаем:
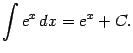
4) Поскольку ![]() , получаем
, получаем
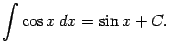
5) Поскольку ![]() , получаем
, получаем
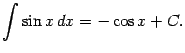
6) Так как ![]() , то
, то
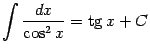
7) Аналогично, поскольку ![]() , получаем
, получаем
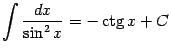
8) Табличная формула ![]() означает, что
означает, что ![]() -- первообразная для
-- первообразная для ![]() на интервале
на интервале ![]() . Значит,
. Значит,
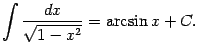
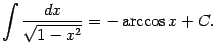
Докажем также обобщение полученной формулы: если ![]() , то на интервале
, то на интервале ![]() имеем
имеем
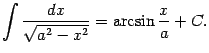
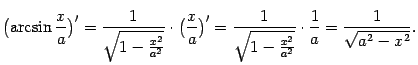
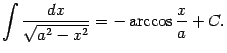
9) Из табличной формулы ![]() (при
(при ![]() ) получаем, что
) получаем, что
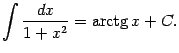
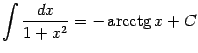
Докажем также следующее обобщение полученной формулы: если ![]() , то
, то
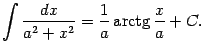
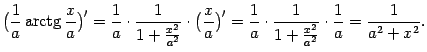
Ясно, что имеет место также формула
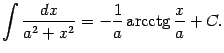
10) Докажем формулу
где
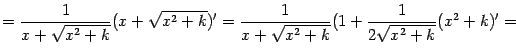 | |
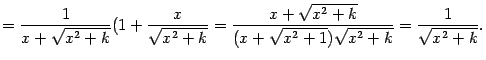 |
Поскольку получили подынтегральную функцию, формула в этом случае доказана. Второй случай, когда
Заметим, что функцию в правой части формулы (1.1) часто называют кдлинным логарифмом", в отличие от правой части формулы следующего пункта, тоже содержащей логарифм.
11) Пусть ![]() и
и ![]() , то есть
, то есть ![]() . Тогда
. Тогда
(здесь
Рассмотрим два случая: ![]() (это неравенство выполняется при
(это неравенство выполняется при ![]() ) и
) и ![]() (это неравенство выполняется при
(это неравенство выполняется при ![]() ). В первом случае имеем
). В первом случае имеем
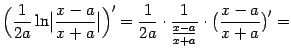 | |
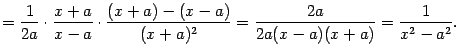 |
Получили подынтегральную функцию, так что формула (1.2) в этом случае доказана. Случай
Функцию, стоящую в правой части формулы (1.2), часто называют квысоким логарифмом".
12) Докажем формулу
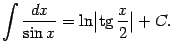
Подсчитаем производную правой части в случае, когда ![]() . Получаем:
. Получаем:
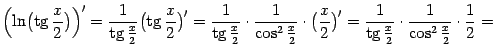 | |
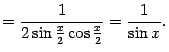 |
Случай
13) Имеет место также формула