‹-- Назад
Производная композиции
Пусть
Теорема 4.4 Если функция 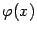 имеет производную
имеет производную 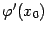 , а функция
, а функция 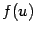 -- производную
-- производную 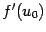 , то композиция
, то композиция 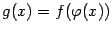 имеет производную
имеет производную
Доказательство. Рассмотрим приращение функции ![]() , соответствующее приращению
, соответствующее приращению ![]() переменного
переменного ![]() :
:
Теперь, в соответствии с теоремой 4.3, осталось доказать, что в последней формуле в квадратных скобках стоит величина, бесконечно малая при
Замечание 4.9 Мы можем пояснить происхождение формулы (4.13), то есть формулы 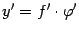 , где
, где 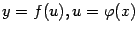 , записав её в виде
, записав её в виде 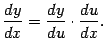 Эта формула получается предельным переходом из очевидного равенства
Эта формула получается предельным переходом из очевидного равенства 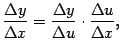 однако такое доказательство формулы (4.13) имеет существенный недостаток, поскольку ниоткуда не следует, что
однако такое доказательство формулы (4.13) имеет существенный недостаток, поскольку ниоткуда не следует, что 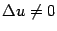 при всех
при всех 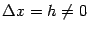 . Тем не менее, смысл формулы для производной композиции функций при этом, несомненно, проясняется.
. Тем не менее, смысл формулы для производной композиции функций при этом, несомненно, проясняется.
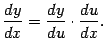
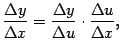
Пример 4.4 Пусть 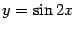 , то есть
, то есть 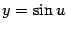 , где
, где 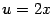 : данная функция представлена в виде композиции функций
: данная функция представлена в виде композиции функций 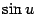 и
и 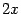 . Тогда для нахождения производной мы можем применить формуду производной композиции. Поскольку
. Тогда для нахождения производной мы можем применить формуду производной композиции. Поскольку 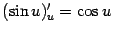 и
и 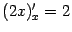 (нижний индекс мы пишем для напоминания о том, по какой переменной берётся производная), то
(нижний индекс мы пишем для напоминания о том, по какой переменной берётся производная), то 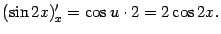 Тот же самый, разумеется, результат мы получим, использовав равенство
Тот же самый, разумеется, результат мы получим, использовав равенство 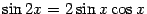 и применив формулу производной произведения:
и применив формулу производной произведения: 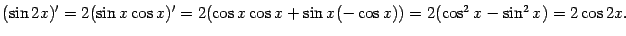 Однако первый способ гораздо продуктивнее: совершенно аналогично получаем, например,
Однако первый способ гораздо продуктивнее: совершенно аналогично получаем, например, 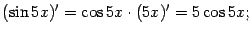
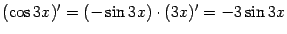 и т. п.
и т. п.
Беря в качестве промежуточного аргумента любую дифференцируемую функцию ![]() , из доказанных ранее формул получаем:
, из доказанных ранее формул получаем:
в частности, | |
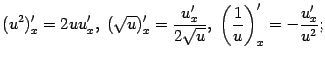 | |
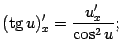 | |
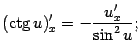 | |
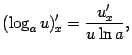 | |
в частности, | |
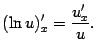 | |
Пример 4.5 Найдём производную функции 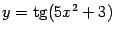 . Здесь промежуточный аргумент равен
. Здесь промежуточный аргумент равен 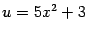 ;
; 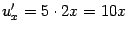 . Поэтому по формуле
. Поэтому по формуле 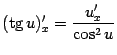 получаем:
получаем: 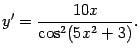
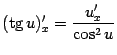 получаем:
получаем: 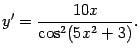
Пример 4.6 Найдём производную функции 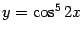 . Здесь функция имеет вид
. Здесь функция имеет вид 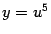 , с промежуточным аргументом
, с промежуточным аргументом 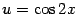 , который, в свою очередь, является сложной функцией. Поэтому
, который, в свою очередь, является сложной функцией. Поэтому 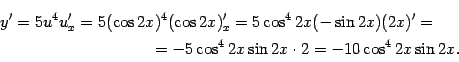
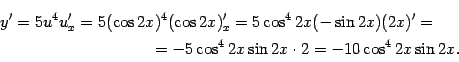
Пример 4.7 Найдём производные ареа-функций (напомним, что ареа-функции -- это функции, обратные к гиперболическим функциям). Ранее мы записали для них следующие формулы:
Поэтому 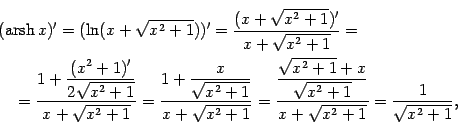
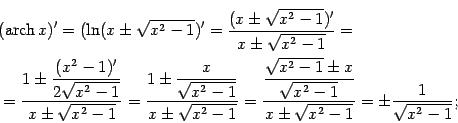
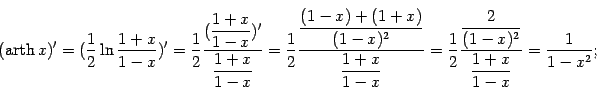
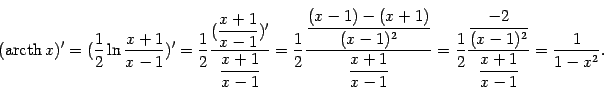
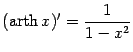 при
при 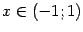 , а
, а 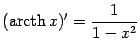 при
при 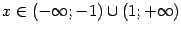 .
.
(в зависимости от того, что считать главной ветвью функции | |
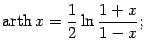 | |
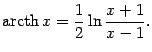 | |
Поэтому
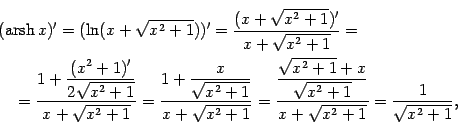
и аналогично:
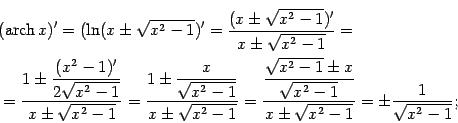
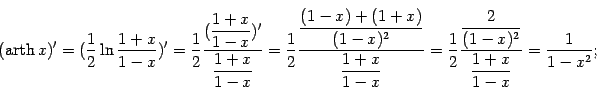
и аналогично:
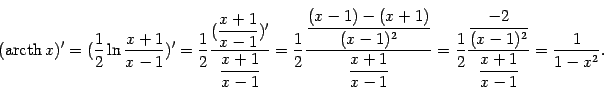
Последние две формулы не противоречат друг другу, так как
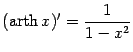 при
при 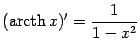 при
при
Упражнение 4.1 Пусть  -- чётная функция, имеющая производную
-- чётная функция, имеющая производную 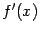 . Докажите, что тогда
. Докажите, что тогда 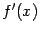 является нечётной функцией. Наоборот, если
является нечётной функцией. Наоборот, если  -- нечётная функция, докажите, что
-- нечётная функция, докажите, что 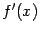 -- чётная функция.
-- чётная функция.
При этом воспользуйтесь тем, что для чётной функции ![]() , а для нечётной функции
, а для нечётной функции ![]() , и примените правило нахождения производной композиции, с промежуточным аргументом
, и примените правило нахождения производной композиции, с промежуточным аргументом ![]() .
.
Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции