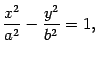‹-- Назад Из школьного курса математики известно, что кривая, задаваемая уравнением

, где

-- число, называется гиперболой. Однако это -- частный случай гиперболы (равносторонняя гипербола).
Определение 12.5 Гиперболой называется геометрическое место точек плоскости, для каждой из которых абсолютная величина разности расстояний до двух фиксированных точек той же плоскости, называемых фокусами гиперболы, есть величина постоянная.
Так же, как и в случае эллипса, для получения уравнения гиперболы выберем подходящую систему координат. Начало координат расположим на середине отрезка между фокусами, ось 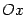 направим вдоль этого отрезка, а ось ординат -- перпендикулярно к нему.
направим вдоль этого отрезка, а ось ординат -- перпендикулярно к нему.
Теорема 12.3 Пусть расстояние между фокусами  и
и  гиперболы равно
гиперболы равно  , а абсолютная величина разности расстояний от точки гиперболы до фокусов равна
, а абсолютная величина разности расстояний от точки гиперболы до фокусов равна  . Тогда гипербола в выбранной выше системе координат имеет уравнение
. Тогда гипербола в выбранной выше системе координат имеет уравнение 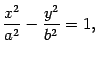 | (12.8) |
где  | (12.9) |
Доказательство. Пусть

-- текущая точка гиперболы (рис. 12.9).

Рис.12.9. Так как разность двух сторон треугольника меньше третьей стороны, то  , то есть
, то есть  ,
,  . В силу последнего неравенства вещественное число
. В силу последнего неравенства вещественное число  , определяемое формулой (12.9), существует.
, определяемое формулой (12.9), существует.
По условию, фокусы --  ,
,  . По формуле (10.4) для случая плоскости получаем
. По формуле (10.4) для случая плоскости получаем
По определению гиперболы
Это уравнение запишем в виде
Обе части возведем в квадрат:
После приведения подобных членов и деления на 4, приходим к равенству
Опять обе части возведем в квадрат:
Раскрывая скобку и приводя подобные члены, получим
С учетом формулы (
12.9) уравнение принимает вид
Разделим обе части уравнения на

и получим уравнение (
12.8)
Уравнение (12.8) называется каноническим уравнением гиперболы.
Предложение 12.3 Гипербола обладает двумя взаимно перпендикулярными осями симметрии, на одной из которых лежат фокусы гиперболы, и центром симметрии. Если гипербола задана каноническим уравнением, то ее осями симметрии служат координатные оси 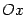 и
и 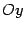 , а начало координат -- центр симметрии гиперболы.
, а начало координат -- центр симметрии гиперболы. Доказательство. Проводится аналогично доказательству
предложения 12.1.
Проведем построение гиперболы, заданной уравнением (12.8). Заметим, что из-за симметрии достаточно построить кривую только в первом координатном угле. Выразим из канонического уравнения 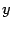 как функцию
как функцию 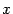 , при условии, что
, при условии, что  ,
,
и построим график этой функции.
Область определения -- интервал  ,
,  , функция монотонно растет. Производная
, функция монотонно растет. Производная
существует во всей области определения, кроме точки

. Следовательно, график -- гладкая кривая (без углов). Вторая производная
во всех точках интервала

отрицательна, следовательно, график -- выпуклый вверх.
Проверим график на наличие асимптоты при  . Пусть асимптота имеет уравнение
. Пусть асимптота имеет уравнение  . Тогда по правилам математического анализа
. Тогда по правилам математического анализа
Выражение под знаком предела домножим и разделим на

. Получим
Итак, график функции имеет асимптоту

. Из симметрии гиперболы следует, что

-- тоже асимптота. Остается неясным характер кривой в окрестности точки

, а именно, образует ли график

и симметричная ему относительно оси
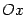
часть гиперболы в этой точке угол или гипербола в этой точке -- гладкая кривая (есть касательная). Для решения этого вопроса выразим из уравнения (
12.8)
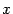
через
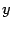
:
Очевидно, что данная функция имеет производную в точке

,

, и в точке

у гиперболы есть вертикальная касательная. По полученным данным рисуем график функции

(рис. 12.10).

Рис.12.10.График функции 
Окончательно, используя симметрию гиперболы, получаем кривую рисунка 12.11.

Рис.12.11.Гипербола
Определение 12.6 Точки пересечения гиперболы, заданной каноническим уравнением (
12.8), с осью
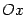
называются
вершинами гиперболы, отрезок между ними называется
действительной осью гиперболы. Отрезок оси ординат между точками

и

называется
мнимой осью. Числа

и

называются соответственно
действительной и
мнимой полуосями гиперболы. Начало координат называется ее
центром. Величина

называется
эксцентриситетом гиперболы.
Замечание 12.3 Из равенства (
12.9) следует, что

, то есть у гиперболы

. Эксцентриситет

характеризует угол между асимптотами, чем ближе

к 1, тем меньше этот угол.
Замечание 12.4 В отличие от эллипса в каноническом уравнении гиперболы соотношение между величинами

и

может быть произвольным. В частности, при

мы получим равностороннюю гиперболу, известную из школьного курса математики. Ее уравнение имеет знакомый вид

, если взять

, а оси

и

направить по биссектрисам четвертого и первого координатных углов (рис. 12.12).

Рис.12.12.Равносторонняя гипербола 
Для отражения на рисунке качественных характеристик гиперболы достаточно определить ее вершины, нарисовать асимптоты и нарисовать гладкую кривую, проходящую через вершины, приближающуюся к асимптотам и похожую на кривую рисунка 12.10.
Пример 12.4 Постройте гиперболу

, найдите ее фокусы и эксцентриситет.
Решение. Разделим обе части уравнения на 4. Получим каноническое уравнение

,

. Проводим асимптоты

и строим гиперболу (рис. 12.13).

Рис.12.13.Гипербола 
Из формулы (12.9) получим  . Тогда фокусы --
. Тогда фокусы --  ,
,  ,
,  .
.
Пример 12.5 Постройте гиперболу

. Найдите ее фокусы и эксцентриситет.
Решение. Преобразуем уравнение к виду
Данное уравнение не является каноническим уравнением гиперболы, так как знаки перед

и

противоположны знакам в каноническом уравнении. Однако, если переобозначить переменные

,

, то в новых переменных получим каноническое уравнение
Действительная ось этой гиперболы лежит на оси

, то есть на оси
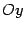
исходной системы координат, асимптоты имеют уравнение

, то есть уравнение

в исходных координатах. Действительная полуось равна 5, мнимая -- 2. В соответствии с этими данными проводим построение (рис. 12.14).

Рис.12.14.Гипербола с уравнением 
Из формулы (12.9) получим  ,
,  , фокусы лежат на действительной оси --
, фокусы лежат на действительной оси --  ,
,  , где координаты указаны в исходной системе координат.
, где координаты указаны в исходной системе координат.
Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции
![]() направим вдоль этого отрезка, а ось ординат -- перпендикулярно к нему.
направим вдоль этого отрезка, а ось ординат -- перпендикулярно к нему. 
![]() , то есть
, то есть ![]() ,
, ![]() . В силу последнего неравенства вещественное число
. В силу последнего неравенства вещественное число ![]() , определяемое формулой (12.9), существует.
, определяемое формулой (12.9), существует. ![]() ,
, ![]() . По формуле (10.4) для случая плоскости получаем
. По формуле (10.4) для случая плоскости получаем ![]() как функцию
как функцию ![]() , при условии, что
, при условии, что ![]() ,
, 
![]() ,
, ![]() , функция монотонно растет. Производная
, функция монотонно растет. Производная 

![]() . Пусть асимптота имеет уравнение
. Пусть асимптота имеет уравнение ![]() . Тогда по правилам математического анализа
. Тогда по правилам математического анализа 






![]() . Тогда фокусы --
. Тогда фокусы -- ![]() ,
, ![]() ,
, ![]() .
. 


![]() ,
, ![]() , фокусы лежат на действительной оси --
, фокусы лежат на действительной оси -- ![]() ,
, ![]() , где координаты указаны в исходной системе координат.
, где координаты указаны в исходной системе координат.