‹-- Назад Рассмотрим линию

в плоскости
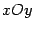
, представленную как график функции
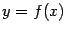
на отрезке
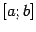
оси

. Предположим, что функция

имеет на отрезке
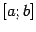
непрерывную производную

.
Пусть поверхность 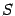 получена как результат вращения в пространстве
получена как результат вращения в пространстве 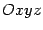 линии
линии  вокруг оси
вокруг оси  (см. рис.). Наша цель -- найти площадь
(см. рис.). Наша цель -- найти площадь  поверхности вращения
поверхности вращения 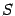 (сделанное построение и полученная при этом формула будут одновременно служить и определением того, что такое площадь поверхности
(сделанное построение и полученная при этом формула будут одновременно служить и определением того, что такое площадь поверхности 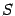 ).
).

Рис.6.19.
Пусть

-- площадь той части поверхности
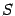
, что проектируется на отрезок

, лежащий на оси

. Очевидно тогда, что

и что

-- это искомая площадь.
Найдём производную функции  , применив для этого определение производной. Придадим значению
, применив для этого определение производной. Придадим значению  переменной
переменной  некоторое приращение
некоторое приращение  и рассмотрим приращение функции
и рассмотрим приращение функции  . Это приращение равно площади части поверхности
. Это приращение равно площади части поверхности 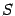 между сечениями этой поверхности плоскостями
между сечениями этой поверхности плоскостями  и
и  (если
(если  , то нужно вдобавок поменять знак). Далее для простоты выкладок будем предполагать
, то нужно вдобавок поменять знак). Далее для простоты выкладок будем предполагать  . Приближённо заменим площадь
. Приближённо заменим площадь  на площадь
на площадь  боковой поверхности усечённого конуса, образующей которого служит хорда графика
боковой поверхности усечённого конуса, образующей которого служит хорда графика 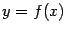 , соединяющая точки
, соединяющая точки  и
и  в плоскости
в плоскости 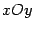 .
.

Рис.6.20.
Тогда
где

и

(мы применили к разности

, стоящей под знаком корня, теорему Лагранжа).
Запишем теперь  в виде
в виде
Во второй и третьей строках этой формулы бесконечно малыми более высокого порядка малости (при  ), чем
), чем 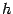 . Действительно,
. Действительно,  при
при  , а величина
, а величина  ограничена в силу непрерывности функции
ограничена в силу непрерывности функции  и её производной
и её производной  . Далее, из непрерывности
. Далее, из непрерывности  следует, что
следует, что  при
при  , а из непрерывности
, а из непрерывности  -- что величина
-- что величина  ограничена. Следовательно, слагаемое в первой строке формулы -- это главная, линейная по
ограничена. Следовательно, слагаемое в первой строке формулы -- это главная, линейная по 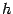 , часть приращения
, часть приращения  , и вместе с ним -- главная часть приращения функции
, и вместе с ним -- главная часть приращения функции  . Напомним теперь, что главная, линейная по
. Напомним теперь, что главная, линейная по 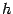 часть приращения функции -- это её дифференциал. Значит,
часть приращения функции -- это её дифференциал. Значит,
Сменив обозначение

на

(ведь

-- произвольная точка
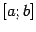
) и
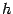
на
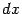
, получаем:
Отсюда
С учётом того, что, как мы отмечали выше,

, получаем:
Наконец, положив

равным
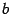
, находим искомую площадь

поверхности вращения:
(мы снова использовали

как обозначение переменной интегрирования).
Замечание 6.1 Заметим, что в процессе преобразований мы приближённо заменили на отрезке

величину

на

, а затем перешли к пределу при

. Это соответствует тому, как если бы мы составили интегральную сумму для функции

(эта интегральная сумма, построенная по размеченному разбиению
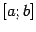
на отрезки длины

, точками разметки в котором служат

, приближённо заменяет нам площадь поверхности тела вращения), а затем перешли к пределу при неограниченном измельчении разбиения и получили в пределе равенство (
6.10). Такой путь получения формулы (
6.10) привёл бы нас к несколько более громоздким выкладкам, хотя и эквивалентен тому, что был использован выше.
Пример 6.9 Вычислим площадь

поверхности, образованной вращением в пространстве вокруг оси

части линии

, расположенной над отрезком

оси

.

Рис.6.21.
Так как

, то формула (
6.10) даёт нам интеграл
Сделаем в последнем интеграле замену

и получим:
В первом из интегралов правой части сделаем замену

:
Для вычисления второго из интегралов в правой части обозначим его

и проинтегрируем по частям, получив уравнение для

, как в
примере 6.6:
Перенося

в левую часть и деля на 2, получаем
откуда, наконец,
Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции
![]() получена как результат вращения в пространстве
получена как результат вращения в пространстве ![]() линии
линии ![]() вокруг оси
вокруг оси ![]() (см. рис.). Наша цель -- найти площадь
(см. рис.). Наша цель -- найти площадь ![]() поверхности вращения
поверхности вращения ![]() (сделанное построение и полученная при этом формула будут одновременно служить и определением того, что такое площадь поверхности
(сделанное построение и полученная при этом формула будут одновременно служить и определением того, что такое площадь поверхности ![]() ).
). 
![]() , применив для этого определение производной. Придадим значению
, применив для этого определение производной. Придадим значению ![]() переменной
переменной ![]() некоторое приращение
некоторое приращение ![]() и рассмотрим приращение функции
и рассмотрим приращение функции ![]() . Это приращение равно площади части поверхности
. Это приращение равно площади части поверхности ![]() между сечениями этой поверхности плоскостями
между сечениями этой поверхности плоскостями ![]() и
и ![]() (если
(если ![]() , то нужно вдобавок поменять знак). Далее для простоты выкладок будем предполагать
, то нужно вдобавок поменять знак). Далее для простоты выкладок будем предполагать ![]() . Приближённо заменим площадь
. Приближённо заменим площадь ![]() на площадь
на площадь ![]() боковой поверхности усечённого конуса, образующей которого служит хорда графика
боковой поверхности усечённого конуса, образующей которого служит хорда графика ![]() , соединяющая точки
, соединяющая точки ![]() и
и ![]() в плоскости
в плоскости ![]() .
. 

![]() в виде
в виде ![]() ), чем
), чем ![]() . Действительно,
. Действительно, ![]() при
при ![]() , а величина
, а величина ![]() ограничена в силу непрерывности функции
ограничена в силу непрерывности функции ![]() и её производной
и её производной ![]() . Далее, из непрерывности
. Далее, из непрерывности ![]() следует, что
следует, что ![]() при
при ![]() , а из непрерывности
, а из непрерывности ![]() -- что величина
-- что величина ![]() ограничена. Следовательно, слагаемое в первой строке формулы -- это главная, линейная по
ограничена. Следовательно, слагаемое в первой строке формулы -- это главная, линейная по ![]() , часть приращения
, часть приращения ![]() , и вместе с ним -- главная часть приращения функции
, и вместе с ним -- главная часть приращения функции ![]() . Напомним теперь, что главная, линейная по
. Напомним теперь, что главная, линейная по ![]() часть приращения функции -- это её дифференциал. Значит,
часть приращения функции -- это её дифференциал. Значит, 










