‹-- Назад
Пример 6.10 Найдём площадь
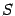
ограниченной области, лежащей между осью

и линией

.
Поскольку  линия пересекает ось
линия пересекает ось  в трёх точках:
в трёх точках:  ,
, 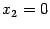 ,
,  .
.

Рис.6.22.
Ограниченная область между линией и осью

проектируется на отрезок

, причём на отрезке

линия

идёт выше оси

(то есть линии

), а на

-- ниже. Поэтому площадь области можно подсчитать так:
Пример 6.11 Найдём площадь
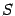
области, заключённой между первым и вторым витком спирали Архимеда

(
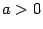
) и отрезком горизонтальной оси

.

Рис.6.25.
Первый виток спирали соответствует изменению угла
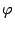
в пределах от 0 до

, а второй -- от

до

. Чтобы привести изменение аргумента
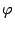
к одному промежутку, запишем уравнение второго витка спирали в виде

,
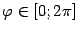
. Тогда площадь
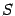
можно будет найти по формуле (
6.4), положив

и

:
Пример 6.12 Найдём объём
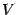
тела, ограниченного поверхностью вращения линии

вокруг оси

(при

).

Рис.6.27.
Для вычисления объёма тела вращения применим формулу
Имеем:
Пример 6.13 Вычислим длину

дуги линии

, расположенной между прямыми
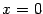
и

.

Рис.6.30.
Так как
и
(мы взяли в качестве значения корня
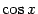
, а не

, поскольку

при

), длина дуги равна
Ответ: 
Пример 6.14 Вычислим площадь

поверхности вращения, полученной при вращении дуги циклоиды

, при

, вокруг оси

.

Рис.6.31.
Для вычисления применим формулу (
6.10):
Имеем:

,

, так что
Для перехода под знаком интеграла к переменной

заметим, что при

получаем

, а также
Кроме того, предварительно вычислим
(так что

) и
Получаем:
Делая замену

, приходим к интегралу
Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции
![]() линия пересекает ось
линия пересекает ось ![]() в трёх точках:
в трёх точках: ![]() ,
, ![]() ,
, ![]() .
. 















![]()








