‹-- Назад

Системы линейных уравнений

        Определение 15.1   Системой 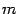$ m$ линейных уравнений с $ n$ неизвестными называется система уравнений вида

$\displaystyle \left\{\begin{array}{l}a_{11}x_1+a_{12}x_2+\ldots+a_{1n}x_n=b_1,\... ...ots\ldots\ldots\\ a_{m1}x_1+a_{m2}x_2+\ldots+a_{mn}x_n=b_m.\end{array}\right.$ (15.1)

Система уравнений называется однородной, если $ {b_1=b_2=\ldots=b_m=0}$ и неоднородной в противном случае.         

Систему (15.1) можно записать также в виде

$\displaystyle a_{i1}x_1+a_{i2}x_2+\ldots+a_{in}x_n=b_i,\quad i=1,2,\dots,m,$

или в виде

$\displaystyle \sum_{j=1}^na_{ij}x_j=b_i,\quad i=1,2,\dots,m.$

Но наиболее удобной формой записи системы (15.1) является матричная запись. Введем следующие матрицы: матрица системы $ a$ , столбец неизвестных $ x$ и столбец свободных членов $ b$ ,

$\displaystyle a=\left(\begin{array}{cccc}a_{11}&a_{12}&\dots&a_{1n}\\ a_{21}&... ...ht), \quad b=\left(\begin{array}{c}b_1\\ b_2\\ \vdots\\ b_m\end{array}\right).$

Читатель, выполнив матричное умножение, легко проверит, что с помощью введенных обозначений систему (15.1) можно записать в виде

$\displaystyle ax=b.$ (15.2)

        Определение 15.2   Решением системы (15.1) называется любой набор чисел $ {{\alpha}_1,\,{\alpha}_2,\dots,{\alpha}_n}$ , которые при подстановке в систему вместо неизвестных $ {x_1,\,x_2,\dots,x_n}$ превращают все уравнения системы в верные равенства.

Решением системы (15.2) называется столбец чисел $ \left(\begin{array}{c}{\alpha}_1\\ {\alpha}_2\\ \vdots\\ {\alpha}_n\end{array}\right)$ , который после подстановки в уравнение вместо столбца $ x$ превращает уравнение (15.2) в верное матричное равенство.         






Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции

на главную
Hosted by uCoz