‹-- Назад В предыдущих примерах мы видели, что хотя необходимое условие не гарантировало наличие экстремума в критической точке, мы смогли исследовать поведение функции в окрестности этой точки и выяснить, имеется ли в ней экстремум и если да, то какого рода. Однако для выяснения этого нам пришлось иной раз прибегать к искусственным преобразованиям функции, которые во общем случае могут быть не очевидны или затруднительны. В данном разделе мы рассмотрим несколько общих теорем, позволяющих исследовать поведение функции в критической точке.
Доказательство. Если  не убывает в
не убывает в  , то
, то  при всех
при всех  , поскольку из непрерывности
, поскольку из непрерывности  . Точно так же,
. Точно так же,  при всех
при всех  . Выберем из чисел
. Выберем из чисел  и
и  наименьшее:
наименьшее:  и рассмотрим симметричную окрестность
и рассмотрим симметричную окрестность  . При
. При  , очевидно,
, очевидно,  , то есть
, то есть  -- точка локального максимума.
-- точка локального максимума.
Вторая половина утверждения теоремы сводится к первой, если положить  и заметить, что функция
и заметить, что функция  не убывает в
не убывает в  и не возрастает в
и не возрастает в  ; локальный максимум функции
; локальный максимум функции  соответствует локальному минимуму функции
соответствует локальному минимуму функции 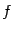 .
.
Замечание 7.4 Найденное достаточное условие локального экстремума гарантирует наличие экстремума в точке

. Однако оно не является необходимым: можно найти такую функцию

, которая имеет экстремум (например, минимум) в некоторой точке

, однако не монотонна ни в какой левой окрестности и ни в какой правой окрестности этой точки. Примером может служить функция
График этой функции зажат между двумя параболами

и

и в окрестности точки 0 имеет бесконечно много промежутков монотонности, разделённых стационарными точками, так что

не монотонна ни на каком интервале вида

или

. В точке 0 функция непрерывна (по теореме "о двух милиционерах") и имеет минимум, так как при всех
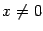

.
Заметим кстати, что производная этой функции равна
Эта производная имеет в точке
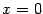
разрыв второго рода.
Теорема 7.6 Пусть  -- критическая точка функции
-- критическая точка функции  , и у этой функции существует производная
, и у этой функции существует производная 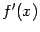 в некоторой проколотой окрестности
в некоторой проколотой окрестности  . Если при этом в левой окрестности
. Если при этом в левой окрестности  имеет место неравенство
имеет место неравенство  , а в правой окрестности
, а в правой окрестности  -- неравенство
-- неравенство  , то точка
, то точка  -- точка локального максимума; если же в левой окрестности выполнено неравенство
-- точка локального максимума; если же в левой окрестности выполнено неравенство  , а в правой окрестности -- неравенство
, а в правой окрестности -- неравенство  , то точка
, то точка  -- точка локального минимума. Наконец, если производная в левой и в правой окрестности имеет один и тот же знак, то точка
-- точка локального минимума. Наконец, если производная в левой и в правой окрестности имеет один и тот же знак, то точка  не является точкой локального экстремума.
не является точкой локального экстремума. Доказательство. Доказательство первых двух утверждений теоремы сразу же следует из предыдущей теоремы и теоремы 7.2 о связи знака производной с возрастанием и убыванием функции: из неравенства  следует неубывание функции
следует неубывание функции  , а из неравенства
, а из неравенства  -- её невозрастание. Последнее утверждение теоремы также очевидно.
-- её невозрастание. Последнее утверждение теоремы также очевидно.

Рис.7.25.Связь смены знака производной с локальными экстремумами
Доказанную теорему можно сформулировать следующим образом:
если производная 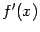 меняет знак с
меняет знак с  на
на  при переходе через критическую точку
при переходе через критическую точку  , то в этой точке -- локальный максимум функции
, то в этой точке -- локальный максимум функции  ; если знак производной меняется с
; если знак производной меняется с  на
на  , то в точке
, то в точке  -- локальный минимум; если же знак производной при переходе через
-- локальный минимум; если же знак производной при переходе через  не изменяется, то локального экстремума в точке
не изменяется, то локального экстремума в точке  функция
функция  не имеет.
не имеет.
Следующая теорема позволяет обойтись для обнаружения экстремума исследованием функции только в точке  (а не в её окрестности, как предыдущие теоремы), но зато требует привлечения второй производной.
(а не в её окрестности, как предыдущие теоремы), но зато требует привлечения второй производной.
Теорема 7.7 Пусть  -- стационарная точка функции
-- стационарная точка функции  , и в этой точке существует вторая производная
, и в этой точке существует вторая производная  , причём
, причём  . Тогда при
. Тогда при  точка
точка  есть точка локального максимума, а при
есть точка локального максимума, а при  -- локального минимума.
-- локального минимума. Доказательство. Поскольку  , то по определению производной
, то по определению производной
Пусть

. Тогда из существования предела следует, что для любого

из некоторой достаточно малой проколотой окрестности

точки

выполняется то же неравенство для допредельного выражения, то есть
при

. Поскольку, по предположению теоремы,

-- стационарная точка, то

, откуда

, то есть
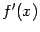
имеет знак, противоположный знаку

:

при

и

при

. Остаётся лишь применить теперь предыдущую теорему, из которой следует, что

-- точка локального максимума.
Доказательство для случая  совершенно аналогично.
совершенно аналогично.
Пример 7.24 Рассмотрим функцию

. Её производная равна

; решая уравнение

, находим стационарные точки функции

: это

. Чтобы определить поведение функции в этих стационарных точках, найдём вторую производную и выясним, какой она имеет знак в каждой из этих трёх точек. Имеем:

. Отсюда

, следовательно, в точке

функция

имеет локальный минимум; то же в точке

, поскольку

также равняется 8. В каждой из этих двух точек значение функции равно

.
В точке  получаем
получаем  , поэтому в точке 0 функция
, поэтому в точке 0 функция  имеет локальный максимум. Значение
имеет локальный максимум. Значение  в этой точке равно 0.
в этой точке равно 0.

Рис.7.26.Три локальных экстремума функции 
Замечание 7.5 В последней теореме ничего не говорится о том, что происходит в стационарной точке

в случае, когда

. В этом случае в точке

может быть как локальный экстремум (возможен и максимум, и минимум), так и не быть экстремума. В этом нас убеждают следующие три примера.
Пример 7.25 Функция

имеет единственную стационарную точку

. Вторая производная

принимает в этой точке значение 0, сама же функция

не имеет экстремума в точке 0.

Рис.7.27.Функция  не имеет экстремума в стационарной точке 0
не имеет экстремума в стационарной точке 0
Пример 7.26 Функция

также имеет единственную стационарную точку
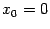
. Вторая производная

принимает в этой точке значение 0, сама же функция

имеет в точке 0 минимум.

Рис.7.28.Функция  имеет минимум в стационарной точке 0, в которой
имеет минимум в стационарной точке 0, в которой 
Пример 7.27 Функция

также имеет единственную стационарную точку
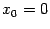
. Её вторая производная

принимает в стационарной точке значение 0, а сама функция

имеет в этой точке максимум.

Рис.7.29.Функция  имеет максимум в стационарной точке 0, в которой
имеет максимум в стационарной точке 0, в которой 
Для того, чтобы разобраться в поведении функции  в такой стационарной точке
в такой стационарной точке  , в которой
, в которой  , можно применить такую теорему:
, можно применить такую теорему:
Доказательство. Для доказательства заметим, что если разложить  по формуле Тейлора в точке
по формуле Тейлора в точке  с остаточным членом в форме Лагранжа, то получим
с остаточным членом в форме Лагранжа, то получим
(где

лежит между
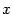
и

), поскольку слагаемые со степенями бинома

, меньшими
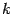
, имеют, по предположению, нулевые коэффициенты. Следовательно, приращение функции

можно представить в виде
Поскольку

и

непрерывна в точке

, то в некоторой окрестности точки

она сохраняет тот же знак, что у числа

, в частности, знак числа

при
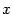
, близких к

, -- тот же, что у числа

.
Мы видим, что при нечётном 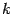 приращение
приращение  меняет знак при переходе через точку
меняет знак при переходе через точку  , поскольку меняет знак множитель
, поскольку меняет знак множитель  в правой части. Значит, в этом случае локального экстремума в точке
в правой части. Значит, в этом случае локального экстремума в точке  нет.
нет.
При чётном 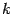 этот множитель положителен при всех
этот множитель положителен при всех  , следовательно, приращение
, следовательно, приращение  (при малых
(при малых  ) имеет тот же знак, что и
) имеет тот же знак, что и  :
:  при
при  (неравенство
(неравенство  означает, что
означает, что  -- точка локального максимума) и
-- точка локального максимума) и  при
при  (неравенство
(неравенство  означает, что
означает, что  -- точка локального минимума).
-- точка локального минимума).
Замечание 7.6 Даже в этом усиленном виде (
теорема 7.8) достаточный признак экстремума, связанный со значениями производных высших порядков, не всегда отвечает на вопрос о том, есть ли локальный экстремум в стационарной точке. Дело в том, что, как мы видели выше, существуют такие функции, у которых
все производные в некоторой точке

обращаются в 0, и тем не менее функция отлична от 0 всюду, кроме этой точки. Примером может служить функция, которую мы рассматривали в главе 6 (замечание 6.2):
Эта функция имеет стационарную точку
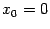
, характер которой нельзя распознать, применив
теорему 7.8, поскольку

при всех
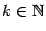
. Однако очевидно, что

при всех
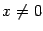
, так что
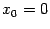
-- точка минимума функции

.
Кроме того, заметим, что может быть не выполнено предположение о непрерывности производной 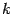 -го порядка в точке
-го порядка в точке  , даже если эта производная существует при всех
, даже если эта производная существует при всех 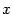 . В качестве примера рассмотрите самостоятельно функцию
. В качестве примера рассмотрите самостоятельно функцию
Эта функция имеет минимум (равный 0) в точке
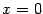
. Производная этой функции существует при всех
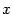
и равна
Найдите и исследуйте вторую производную этой функции.
Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции
![]() не возрастает в некоторой левой окрестности
не возрастает в некоторой левой окрестности ![]() и не убывает в некоторой правой окрестности
и не убывает в некоторой правой окрестности ![]() , то точка
, то точка ![]() -- точка локального минимума.
-- точка локального минимума. ![]() не убывает в
не убывает в ![]() , то
, то ![]() при всех
при всех ![]() , поскольку из непрерывности
, поскольку из непрерывности ![]() . Точно так же,
. Точно так же, ![]() при всех
при всех ![]() . Выберем из чисел
. Выберем из чисел ![]() и
и ![]() наименьшее:
наименьшее: ![]() и рассмотрим симметричную окрестность
и рассмотрим симметричную окрестность ![]() . При
. При ![]() , очевидно,
, очевидно, ![]() , то есть
, то есть ![]() -- точка локального максимума.
-- точка локального максимума. ![]() и заметить, что функция
и заметить, что функция ![]() не убывает в
не убывает в ![]() и не возрастает в
и не возрастает в ![]() ; локальный максимум функции
; локальный максимум функции ![]() соответствует локальному минимуму функции
соответствует локальному минимуму функции ![]() .
. 

![]() следует неубывание функции
следует неубывание функции ![]() , а из неравенства
, а из неравенства ![]() -- её невозрастание. Последнее утверждение теоремы также очевидно.
-- её невозрастание. Последнее утверждение теоремы также очевидно. 
![]() меняет знак с
меняет знак с ![]() на
на ![]() при переходе через критическую точку
при переходе через критическую точку ![]() , то в этой точке -- локальный максимум функции
, то в этой точке -- локальный максимум функции ![]() ; если знак производной меняется с
; если знак производной меняется с ![]() на
на ![]() , то в точке
, то в точке ![]() -- локальный минимум; если же знак производной при переходе через
-- локальный минимум; если же знак производной при переходе через ![]() не изменяется, то локального экстремума в точке
не изменяется, то локального экстремума в точке ![]() функция
функция ![]() не имеет.
не имеет. ![]() (а не в её окрестности, как предыдущие теоремы), но зато требует привлечения второй производной.
(а не в её окрестности, как предыдущие теоремы), но зато требует привлечения второй производной. ![]() , то по определению производной
, то по определению производной 

 , то есть
, то есть ![]() совершенно аналогично.
совершенно аналогично. ![]() получаем
получаем ![]() , поэтому в точке 0 функция
, поэтому в точке 0 функция ![]() имеет локальный максимум. Значение
имеет локальный максимум. Значение ![]() в этой точке равно 0.
в этой точке равно 0. 



![]() в такой стационарной точке
в такой стационарной точке ![]() , в которой
, в которой ![]() , можно применить такую теорему:
, можно применить такую теорему: ![]() по формуле Тейлора в точке
по формуле Тейлора в точке ![]() с остаточным членом в форме Лагранжа, то получим
с остаточным членом в форме Лагранжа, то получим 

 при
при ![]() приращение
приращение ![]() меняет знак при переходе через точку
меняет знак при переходе через точку ![]() , поскольку меняет знак множитель
, поскольку меняет знак множитель ![]() в правой части. Значит, в этом случае локального экстремума в точке
в правой части. Значит, в этом случае локального экстремума в точке ![]() нет.
нет. ![]() этот множитель положителен при всех
этот множитель положителен при всех ![]() , следовательно, приращение
, следовательно, приращение ![]() (при малых
(при малых ![]() ) имеет тот же знак, что и
) имеет тот же знак, что и ![]() :
: ![]() при
при ![]() (неравенство
(неравенство ![]() означает, что
означает, что ![]() -- точка локального максимума) и
-- точка локального максимума) и ![]() при
при ![]() (неравенство
(неравенство ![]() означает, что
означает, что ![]() -- точка локального минимума).
-- точка локального минимума). 
![]() -го порядка в точке
-го порядка в точке ![]() , даже если эта производная существует при всех
, даже если эта производная существует при всех ![]() . В качестве примера рассмотрите самостоятельно функцию
. В качестве примера рассмотрите самостоятельно функцию 
