‹-- Назад
Обзор некоторых элементарных функций
Для напоминания и повторения приведём обзор некоторых функций, изучаемых в школьной программе.1. Линейная функция. Это функция вида 
. Число 
называется угловым коэффициентом, а число 
-- свободным членом. Графиком 
линейной функции служит прямая на координатной плоскости 
, не параллельная оси 
.
Угловой коэффициент равен тангенсу угла 
наклона графика к горизонтальному направлению -- положительному направлению оси 
.
2. Квадратичная функция. Это функция вида 
(
).
Графиком квадратичной функции служит парабола с осью, параллельной оси . При 
вершина параболы оказывается в точке 
.
(
) В общем случае вершина лежит в точке 
. Если , то "рога" параболы направлены вверх, если 
, то вниз.
() 3. Степенная функция. Это функция вида 
, 
. Рассматриваются такие случаи:
а). Если 
, то 
. Тогда 
, 
; если число -- чётное, то и функция 
-- чётная (то есть 
при всех 
); если число -- нечётное, то и функция -- нечётная (то есть 
при всех ).
б). Если 
, 
, то 
. Ситуация с чётностью и нечётностью при этом такая же, как и для 
: если -- чётное число, то и 
-- чётная функция; если -- нечётное число, то и 
-- нечётная функция.
Снова заметим, что при всех . Если 
, то 
при всех 
, кроме 
(выражение 
не имеет смысла).
в). Если -- не целое число, то, по определению, при : 
; тогда , .
При 
, по определению, 
; тогда .
4. Многочлен. Это функция вида 
, где 
, 
. Число 
называется степенью многочлена. При 
и 
многочлены являются соответственно линейной функцией и квадратичной функцией (квадратным трёхчленом) и рассмотрены выше. При 
и 
( 
) получается степенная функция, которую мы также рассмотрели выше. В общем случае ; при чётном значении степени 
характерный вид графика таков:
или таков:
а при нечётном значении степени -- таков:
или таков:
5. Показательная функция (экспонента). Это функция вида 
(, 
). Для неё , 
, 
, и при 
график имеет такой вид:
При 
вид графика такой:
Число 
называется основанием показательной функции.
6. Логарифмическая функция. Это функция вида 
(, ). Для неё , 
, 
, и при график имеет такой вид:
При график получается такой:
Число называется основанием логарифма. Обратим внимание читателя на то, что с точностью до поворотов и симметричных отражений на последних четырёх чертежах изображена одна и та же линия.
7. Функция синус: 
. Для неё ; функция периодична с периодом 
и нечётна. Её график таков:
8. Функция косинус: 
. Эта функция связана с синусом формулой приведения: 
; ; период функции 
равен ; функция чётна. Её график таков:
9. Функция тангенс: 
(в англоязычной литературе обозначается также 
). По определению,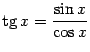 
. Функция 
нечётна и периодична с периодом 
;
не может принимать значений 
, 
, при которых (стоящий в знаменателе) обращается в ноль. 
10. Функция котангенс: 
(в англоязычной литературе также 
). По определению, 
. Если 
( ), то 
. Функция 
нечётна и периодична с периодом ;
не может принимать значения вида 
, , при которых обращается в 0. 
11. Абсолютная величина (модуль): 
, . Эта функция определяет расстояние на вещественной оси от точки 
до точки 0:
чётная, её график такой: 
12. Обратные тригонометрические функции. Это функции арксинус, арккосинус, арктангенс и арккотангенс. Они определяются как функции, обратные к главным ветвям синуса, косинуса, тангенса и котангенса соответственно, о чём подробнее в конце главы, в разделе Обратная функция.
13. Расстояние до начала координат на плоскости и в пространстве. На координатной плоскости 
расстояние 
от точки 
до точки определяется по формуле 
(по теореме Пифагора) и, следовательно, задаёт функцию
построен в примере 1.8. Аналогично, расстояние в пространстве 
от точки 
до точки 
определяется по формуле 
и задаёт функцию
14. Арифметическая прогрессия. Функция 
, задаваемая формулой
, 
-- фиксированные числа, а 
, называется арифметической прогрессией. Число 
называется при этом первым членом прогрессии, а число 
-- разностью прогрессии. Функцию можно представить как ограничение на множество натуральных чисел 
линейной функции 
с угловым коэффициентом и свободным членом 
. Арифметическую прогрессию можно задать и другим, рекуррентным способом: 
при 
. 
15. Геометрическая прогрессия. Функция , задаваемая формулой
, 
-- фиксированные числа, а , называется геометрической прогрессией. Число называется при этом первым членом прогрессии, а число 
-- знаменателем прогрессии. Функцию (при 
, 
) можно представить как ограничение на множество натуральных чисел показательной функции с основанием , умноженной на постоянный коэффициент 
, то есть функции 
Геометрическую прогрессию можно задать и иначе, рекуррентным способом:
при
