‹-- Назад
Аффинное 
-мерное пространство
Если в обычном трехмерном пространстве выбрана система координат Oxyz , то каждая точка 
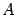
этого пространства отождествлялась с тройкой чисел -- координатами вектора 
. Аналогично мы можем считать, что набор из чисел является точкой -мерного пространства и рассматривать этот набор как координаты радиус-вектора этой точки. Такое -мерное пространство в отличие от векторного называется аффинным -мерным пространством. За начало координат принимается точка 
. За единичные векторы на осях координат в этом случае принимаются радиус-векторы точек
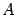
и 
аффинного пространства можно сопоставить вектор 
из -мерного линейного пространства. Для получения координат вектора нужно из координат конца вектора вычесть координаты начала.
, 
-- точки четырехмерного пространства. Тогда вектор имеет координатный столбец 
. Параллельный перенос осей координат осуществляется по формулам, аналогичным (13.21). Пусть точка 
, являющаяся началом новой системы координат, имеет координаты 
. Пусть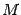 
-- некоторая точка пространства с координатами 
в старой системе координат и 
в новой системе координат. Тогда связь между старыми и новыми координатами задается формулами
В трехмерном пространстве уравнение 
задает плоскость. Аналогично в -мерном пространстве уравнение
где
-- числа, задает плоскость размерности 
, обычно ее называют гиперплоскостью. В трехмерном пространстве система из двух уравнений задает прямую. В -мерном пространстве система
из
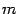
уравнений, 
, задает плоскость размерности 
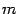
, если ранг матрицы системы равен . Если для векторов задано скалярное произведение формулой (18.3), то в аффинном пространстве можно определять расстояние между точками. Пусть 
, 
-- точки пространства, тогда расстояние между ними
-мерном вещественном пространстве 
-мерную сферу, а неравенство
задает
-мерный шар радиуса 
с центром в начале координат. В аффинном -мерном пространстве можно рассматривать поверхности второго порядка. Их типов оказывается тоже конечное число. Можно рассматривать множество точек, задаваемых уравнением 
. При некоторых ограничениях на функцию 
, это уравнение будет определять -мерную поверхность (гиперповерхность), а неравенство 
-- область в -мерном аффинном пространстве.
