‹-- Назад
Методы, связанные с приближённым нахождением корня производной
Как уже отмечалось выше, если известно, что точка локального экстремума функции 
на отрезке 
единственна и лежит внутри отрезка, то в этой точке 
выполняется равенство 
. Таким образом, для нахождения точки локального минимума с точностью 
нужно с этой точностью найти корень уравнения 
. Будем предполагать, что для функции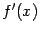 
известно аналитическое выражение или мы умеем вычислять значения 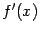при заданном 
каким-либо иным способом. Для нахождения корня мы можем применить один из приближённых методов решения уравнений, которые мы обсуждали в этой главе ранее.
Например, метод Ньютона, применённый к уравнению , даёт итерационную формулу (см. формулу (9.1)):
, причём для начала итераций нужно выбрать начальное приближение 
. При этом нужно будет уметь вычислять и вторую производную, а также предполагать, что она не обращается в 0 на интересующем нас отрезке. Метод хорд даёт итерационную формулу (см. формулу (9.3)):
, причём для начала нужно выбрать два начальных значения и 
. Эти методы весьма эффективны, если выполняются условия их применимости. Их достоинства и недостатки -- продолжение тех же свойств соответствующих методов приближённого поиска корня.
. Производная этой функции равна 
. Нетрудно видеть, вычислив, например, значения функции в точках 
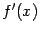
, что функция имеет три корня 
, отделённых, соответственно, на отрезках 
(больше трёх корней многочлен третьей степени иметь не может). При переходе через каждый из этих корней производная меняет знак. Значит, функция имеет три локальных экстремума. Поскольку 
при 
, то нетрудно сообразить, что в точках 
и 
функция будет иметь локальный минимум, а в точке 
-- локальный максимум. Один из двух локальных минимумов будет давать минимальное значение функции на всей оси 
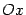
. Осталось найти точки 
и , вычислить в них значения функции и сравнить эти значения.
Точки 
будем искать как корни уравнения , применяя метод Ньютона. Поскольку 
, то итерационная формула метода Ньютона для поиска любой из трёх точек будет иметь вид
, брать 
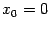
в качестве начального приближения нельзя. Точка отделена на отрезке 
, значит, возьмём за начальное приближение 
. Далее, применяя итерационную формулу, получаем (с точностью 
):
; вычисление значения функции даёт локальный минимум 
. Беря за начальное приближение 
, получаем последовательные приближения к :
; значение локального максимума таково: 
. Теперь возьмём за начальное приближение для значение 
. Получаем последовательные приближения
и значение локального минимума равно 
. Сравнивая два значения в точках локального минимума, получаем, что
неизвестны, но мы умеем вычислять значения самой функции , можно попробовать воспользоваться формулами численного дифференцирования, которые мы обсуждали ранее, например: 
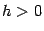
достаточно малое число (но не слишком уж малое: ранее мы видели, что выбор слишком малого шага в формулах численного дифференцирования приводит к большим погрешностям). Конечно, если мы применяем вместо производных их конечно-разностные аналоги, вычисленные с шагом 
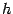
, то нельзя надеяться, что приближённое значение 
для может быть найдено с точностью 
. Поэтому следует выбирать 
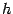
при заданной точности , а поскольку на есть ограничения снизу, то мы видим, что добиться таким образом очень малой погрешности при нахождении точки экстремума нельзя.
