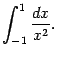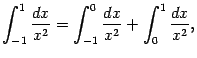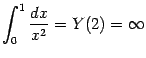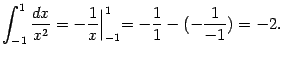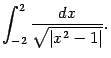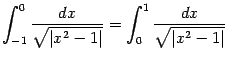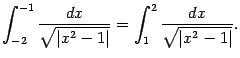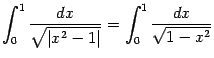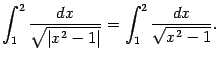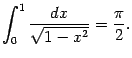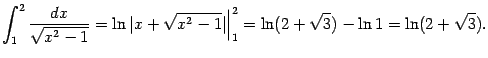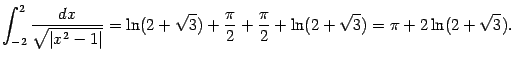‹-- Назад Рассмотрим функцию

и такой промежуток
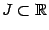
, на котором

имеет несколько особенностей. Будем считать, что
особенности имеются в тех точках промежутка, при приближении к которым функция имеет неинтегрируемые разрывы
11, а также в
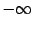
и
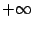
, если они являются концами рассматриваемого промежутка
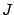
.
Итак, пусть  имеет особенности в
имеет особенности в 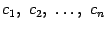 , где, возможно,
, где, возможно, 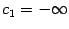 и
и 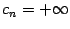 , а все оставшиеся
, а все оставшиеся 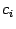 -- точки оси
-- точки оси  . Точки
. Точки 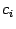 разбивают промежуток
разбивают промежуток 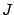 на части -- интервалы
на части -- интервалы 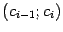 , где внутри интервалов функция уже не имеет особенностей, то есть интегрируема по любому отрезку
, где внутри интервалов функция уже не имеет особенностей, то есть интегрируема по любому отрезку 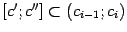 . Если промежуток
. Если промежуток 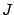 -- это отрезок
-- это отрезок 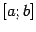 и в точках
и в точках 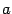 и
и 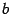 функция не имеет особенностей, то к интервалам
функция не имеет особенностей, то к интервалам 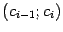 добавляются ещё полуинтервалы
добавляются ещё полуинтервалы 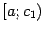 и
и 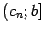 с особенностями только в точках
с особенностями только в точках 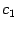 и
и 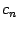 . Выберем в каждом из интервалов
. Выберем в каждом из интервалов 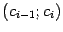 по точке
по точке 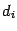 . Тогда на полуинтервалах
. Тогда на полуинтервалах 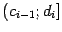 и
и 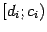 функция
функция  имеет ровно по одной особенности -- в точке
имеет ровно по одной особенности -- в точке 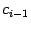 или
или 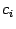 соответственно. Присоединим, если нужно, к этим полуинтервалам ещё и
соответственно. Присоединим, если нужно, к этим полуинтервалам ещё и 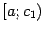 и
и 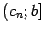 , то есть будем считать в этом случае
, то есть будем считать в этом случае 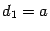 и
и 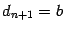 .
.
Определение 4.9 При описанных выше условиях на функцию

и выбор точек
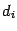
будем считать несобственный интеграл от

по промежутку
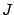
равным сумме несобственных интегралов по каждому из упоминавшихся выше полуинтервалов
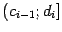
и
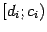
, при условии, что все эти интегралы сходятся:
Если же хотя бы одно из этих слагаемых представляет собою расходящийся интеграл, то интеграл
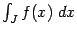
считается расходящимся.
Заметим, что мы уже давали аналогичное определение в случае, когда 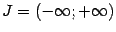 и этот интервал разбивается точкой деления
и этот интервал разбивается точкой деления 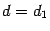 на две части, то есть особенности имеются только в
на две части, то есть особенности имеются только в 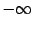 и
и 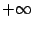 ( определение 4.3). Вслед за тем мы проверили, что величина интеграла при определении 4.3 не зависит от выбора точки деления
( определение 4.3). Вслед за тем мы проверили, что величина интеграла при определении 4.3 не зависит от выбора точки деления 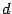 . Аналогичный результат верен и для общего определения 4.9. Доказывается он точно так же, на основе свойства аддитивности определённого интеграла, поэтому мы опускаем доказательство.
. Аналогичный результат верен и для общего определения 4.9. Доказывается он точно так же, на основе свойства аддитивности определённого интеграла, поэтому мы опускаем доказательство.
Пример 4.16 Рассмотрим интеграл
На промежутке интегрирования
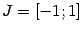
функция
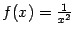
имеет особенность в точке
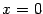
, поскольку
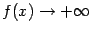
при
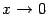
. Точка
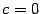
разбивает
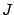
на две части:
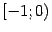
и
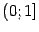
, причём у каждого из этих полуинтервалов лишь один конец (а именно, 0) соответствует особенности функции. Согласно определению, нужно положить
причём нужно проверить сходимость интегралов в правой части. Имеем:
(см. выше,
пример 4.9). Поскольку этот интеграл расходится, то расходится и данный интеграл
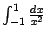
, и проверять сходимость слагаемого
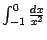
уже нет нужды (на самом деле он тоже расходится).
Заметим, что было бы абсолютно неверно "не заметить" особенность функции в точке 0 и необоснованно применить формулу Ньютона - Лейбница, которая верна только для непрерывных подынтегральных функций:
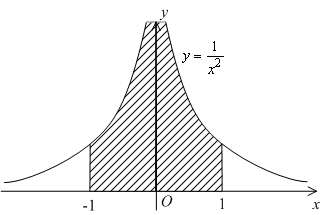
Рис.4.10.
Мало того, что получился абсурдный результат: интеграл от положительной функции
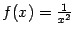
оказался отрицательным, так ещё при таком "способе" счёта мы упустили, что на самом деле площадь под графиком
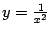
бесконечна.
Пример 4.17 Рассмотрим интеграл
На отрезке
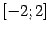
функция имеет две особенности -- в точках
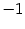
и 1. Поэтому нужно взять ещё точку на интервале между особенностями (возьмём 0 для симметричности), и отрезок разбивается на четыре части:
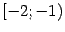
,
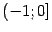
,
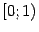
и
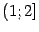
. Интегралы по этим отрезкам -- это несобственные интегралы второго рода, причём в силу чётности подынтегральной функции нам достаточно найти лишь
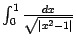
и
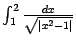
, а остальные два будут иметь те же значения:
и
Заметим, что на промежутке
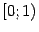
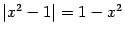
, а на промежутке
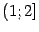
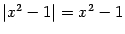
, так что
и
Первый из этих интегралов мы уже вычислили в
примере 4.8:
Вычислим второй:
Итак,
Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции
![]() имеет особенности в
имеет особенности в ![]() , где, возможно,
, где, возможно, ![]() и
и ![]() , а все оставшиеся
, а все оставшиеся ![]() -- точки оси
-- точки оси ![]() . Точки
. Точки ![]() разбивают промежуток
разбивают промежуток ![]() на части -- интервалы
на части -- интервалы ![]() , где внутри интервалов функция уже не имеет особенностей, то есть интегрируема по любому отрезку
, где внутри интервалов функция уже не имеет особенностей, то есть интегрируема по любому отрезку ![]() . Если промежуток
. Если промежуток ![]() -- это отрезок
-- это отрезок ![]() и в точках
и в точках ![]() и
и ![]() функция не имеет особенностей, то к интервалам
функция не имеет особенностей, то к интервалам ![]() добавляются ещё полуинтервалы
добавляются ещё полуинтервалы ![]() и
и ![]() с особенностями только в точках
с особенностями только в точках ![]() и
и ![]() . Выберем в каждом из интервалов
. Выберем в каждом из интервалов ![]() по точке
по точке ![]() . Тогда на полуинтервалах
. Тогда на полуинтервалах ![]() и
и ![]() функция
функция ![]() имеет ровно по одной особенности -- в точке
имеет ровно по одной особенности -- в точке ![]() или
или ![]() соответственно. Присоединим, если нужно, к этим полуинтервалам ещё и
соответственно. Присоединим, если нужно, к этим полуинтервалам ещё и ![]() и
и ![]() , то есть будем считать в этом случае
, то есть будем считать в этом случае ![]() и
и ![]() .
. 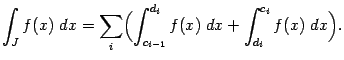
![]() и этот интервал разбивается точкой деления
и этот интервал разбивается точкой деления ![]() на две части, то есть особенности имеются только в
на две части, то есть особенности имеются только в ![]() и
и ![]() ( определение 4.3). Вслед за тем мы проверили, что величина интеграла при определении 4.3 не зависит от выбора точки деления
( определение 4.3). Вслед за тем мы проверили, что величина интеграла при определении 4.3 не зависит от выбора точки деления ![]() . Аналогичный результат верен и для общего определения 4.9. Доказывается он точно так же, на основе свойства аддитивности определённого интеграла, поэтому мы опускаем доказательство.
. Аналогичный результат верен и для общего определения 4.9. Доказывается он точно так же, на основе свойства аддитивности определённого интеграла, поэтому мы опускаем доказательство.