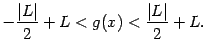‹-- Назад
Общие свойства пределов
В этом разделе мы на основе изученных выше свойств бесконечно малых величин (то есть функций, имеющих предел, равный 0) выясним свойства функций, имеющих произвольное значение предела.
Доказательство. Равенство ![]() означает, в соответствии с теоремой 2.4, что величина
означает, в соответствии с теоремой 2.4, что величина ![]() -- бесконечно малая; равенство
-- бесконечно малая; равенство ![]() -- что
-- что ![]() -- бесконечно малая. Поэтому по теореме 2.5 сумма
-- бесконечно малая. Поэтому по теореме 2.5 сумма
Так что из несуществования пределов слагаемых не следует несуществование предела суммы.
Доказательство. Равенство ![]() означает, в соответствии с теоремой 2.4, что величина
означает, в соответствии с теоремой 2.4, что величина ![]() -- бесконечно малая; равенство
-- бесконечно малая; равенство ![]() -- что
-- что ![]() -- бесконечно малая. Поэтому
-- бесконечно малая. Поэтому ![]() и
и ![]() , откуда
, откуда
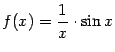 при
при Так что из несуществования предела у какого-нибудь сомножителя не следует несуществование предела произведения.
Доказательство. Для доказательства достаточно заметить, что, согласно примеру 2.4, ![]() , и применить теорему 2.9.
, и применить теорему 2.9.
Доказанное следствие означает, что постоянный множитель ![]() можно выносить за знак предела, а также вносить под знак предела. Иными словами, умножение на постоянную и переход к пределу можно менять местами.
можно выносить за знак предела, а также вносить под знак предела. Иными словами, умножение на постоянную и переход к пределу можно менять местами.
Доказательство. Оно состоит в последовательном ![]() -кратном применении теоремы 2.8 к слагаемым
-кратном применении теоремы 2.8 к слагаемым ![]() , предел которых, согласно предыдущему следствию, равен
, предел которых, согласно предыдущему следствию, равен ![]() .
.
В качестве частного случая можно рассмотреть предел разности двух функций. Разность ![]() можно представить в виде
можно представить в виде ![]() и применить следствие 2.5 к этой сумме из двух слагаемых. Получим тогда, что
и применить следствие 2.5 к этой сумме из двух слагаемых. Получим тогда, что
Предел отношения двух функций ![]() , в отличие от суммы, разности и произведения, не обязательно равен отношению пределов числителя
, в отличие от суммы, разности и произведения, не обязательно равен отношению пределов числителя ![]() и знаменателя
и знаменателя ![]() , даже если пределы
, даже если пределы ![]() и
и ![]() существуют. Дело в том, что предел знаменателя может равняться нулю, и отношение пределов тогда не имеет смысла, в то время как предел отношения
существуют. Дело в том, что предел знаменателя может равняться нулю, и отношение пределов тогда не имеет смысла, в то время как предел отношения 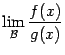 при этом вполне может существовать. Приведём такой простейший пример:
при этом вполне может существовать. Приведём такой простейший пример:
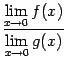 не имеет смысла. При этом
не имеет смысла. При этом 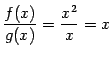 при
при 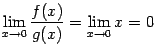 .
. Оказывается, условия ![]() , которое обеспечивает то, что отношение пределов имеет смысл, -- этого условия достаточно для того, чтобы предел отношения двух функций был равен отношению их пределов. Ниже мы докажем соответствующую теорему, а пока докажем такое вспомогательное утверждение.
, которое обеспечивает то, что отношение пределов имеет смысл, -- этого условия достаточно для того, чтобы предел отношения двух функций был равен отношению их пределов. Ниже мы докажем соответствующую теорему, а пока докажем такое вспомогательное утверждение.
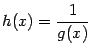 определена на некотором окончании этой базы и локально ограничена при этой базе.
определена на некотором окончании этой базы и локально ограничена при этой базе. Доказательство. Возьмём положительное число 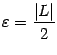 . По определению предела, в базе
. По определению предела, в базе ![]() найдётся такое окончание
найдётся такое окончание ![]() , что при всех
, что при всех ![]() будет
будет 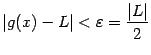 . Это неравенство можно привести к виду
. Это неравенство можно привести к виду
При ![]() это неравенство означает, что
это неравенство означает, что 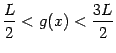 ; так как
; так как ![]() , то и
, то и ![]() при всех
при всех ![]() и, следовательно, функция
и, следовательно, функция 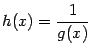 определена во всех точках окончания
определена во всех точках окончания ![]() и удовлетворяет неравенству
и удовлетворяет неравенству
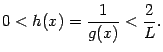
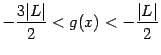 ; так как
; так как 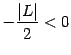 , то и
, то и 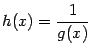 определена во всех точках окончания
определена во всех точках окончания 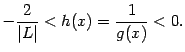
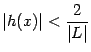 , что означает локальную ограниченность функции
, что означает локальную ограниченность функции На основе этой леммы мы докажем обещанное выше утверждение о пределе отношения.
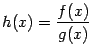 определена на некотором окончании базы
определена на некотором окончании базы 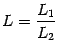 , то есть предел отношения равен отношению пределов числителя и знаменателя.
, то есть предел отношения равен отношению пределов числителя и знаменателя. Доказательство. Представим отношение ![]() в виде
в виде 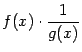 , в котором и первый, и второй множители определены на некотором окончании
, в котором и первый, и второй множители определены на некотором окончании ![]() базы
базы ![]() (относительно второго множителя см. предыдущую лемму). Поэтому и исходное отношение имеет смысл при всех
(относительно второго множителя см. предыдущую лемму). Поэтому и исходное отношение имеет смысл при всех ![]() .
.
Утверждение о том, что 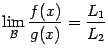 , эквивалентно тому, что разность
, эквивалентно тому, что разность 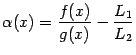 -- бесконечно малая величина. Приводя эту разность к общему знаменателю, получим, что
-- бесконечно малая величина. Приводя эту разность к общему знаменателю, получим, что 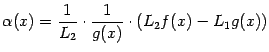 . Величина
. Величина ![]() -- постоянная и, следовательно (см. пример 2.11), локально ограничена; функция
-- постоянная и, следовательно (см. пример 2.11), локально ограничена; функция ![]() -- тоже локально ограничена при базе
-- тоже локально ограничена при базе ![]() (по предыдущей лемме). Значит, с учётом предложения 2.1 и теоремы 2.7, будет доказано, что величина
(по предыдущей лемме). Значит, с учётом предложения 2.1 и теоремы 2.7, будет доказано, что величина ![]() бесконечно малая, если мы покажем, что бесконечно мала при базе
бесконечно малая, если мы покажем, что бесконечно мала при базе ![]() величина
величина ![]() . Найдём предел этой величины. По свойству линейности предела ( следствие 2.5)
. Найдём предел этой величины. По свойству линейности предела ( следствие 2.5)
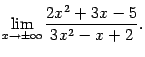
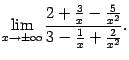
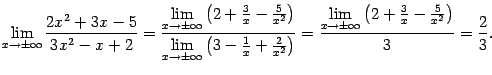 |
Предел числителя, равный 2, мы нашли аналогично пределу знаменателя, пользуясь линейностью предела.
Итак,
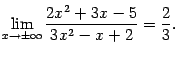
Заметим, что предел отношения многочленов оказался равен отношению коэффициентов при старшей степени ![]() , то есть, в данном случае, при
, то есть, в данном случае, при ![]() .
.
Аналогично решаются и другие примеры на вычисление пределов отношения двух многочленов при ![]() , а также пределов отношения некоторых других функций, например, связанных с корнями из многочленов.
, а также пределов отношения некоторых других функций, например, связанных с корнями из многочленов.
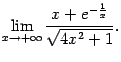
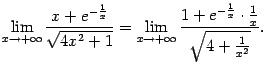
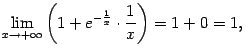
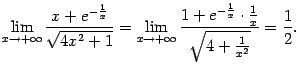
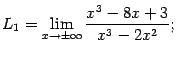
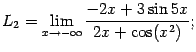
Ответ: ![]() ;
; ![]() ;
; ![]() .
.
Указания: поделите числитель и знаменатель дроби в первом примере на ![]() , во втором -- на
, во втором -- на ![]() и в третьем -- на
и в третьем -- на ![]() . Во втором примере воспользуйтесь тем, что
. Во втором примере воспользуйтесь тем, что ![]() и
и ![]() -- величины, ограниченные при всех
-- величины, ограниченные при всех ![]() (и, следовательно, локально ограниченные при любой базе).
(и, следовательно, локально ограниченные при любой базе).
Доказательство. Согласно определению предела, для любого ![]() найдутся такие окончания базы
найдутся такие окончания базы ![]() и
и ![]() , что при
, что при ![]() выполняется неравенство
выполняется неравенство
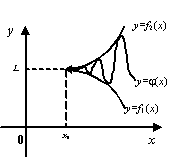
(Происхождение названия теоремы таково: пусть график функции ![]() -- это траектория движения первого милиционера в участок, график
-- это траектория движения первого милиционера в участок, график ![]() -- второго милиционера туда же, а график
-- второго милиционера туда же, а график ![]() -- траектория движения нетрезвого гражданина, находящегося, в соответствии с неравенством
-- траектория движения нетрезвого гражданина, находящегося, в соответствии с неравенством
Доказательство. Если бы предел ![]() был отрицательным, то можно было бы взять
был отрицательным, то можно было бы взять ![]() и найти такое окончание базы
и найти такое окончание базы ![]() , что при
, что при ![]() выполняется неравенство
выполняется неравенство ![]() , откуда
, откуда ![]() . Это же будет выполнено на некотором окончании
. Это же будет выполнено на некотором окончании ![]() , что противоречит предположению, что
, что противоречит предположению, что ![]() при всех
при всех ![]() . Противоречие доказывает, что отрицательным предел
. Противоречие доказывает, что отрицательным предел ![]() быть не может, то есть
быть не может, то есть ![]() .
.
Доказательство. Для доказательства достаточно взять функцию ![]() , применить к ней доказанную только что теорему и воспользоваться тем, что знак минус можно вынести за знак предела (по свойству линейности предела).
, применить к ней доказанную только что теорему и воспользоваться тем, что знак минус можно вынести за знак предела (по свойству линейности предела).
Доказательство. Рассмотрим функцию ![]() . По условию теоремы,
. По условию теоремы, ![]() , причём
, причём
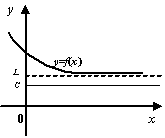
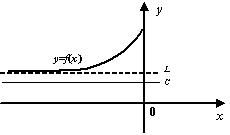
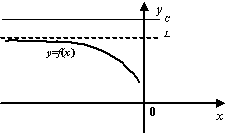
Напомним, что функция ![]() называется не убывающей на множестве
называется не убывающей на множестве ![]() , если для любых
, если для любых ![]() , таких что
, таких что ![]() , выполняется неравенство
, выполняется неравенство ![]() , и не возрастающей на
, и не возрастающей на ![]() , если при
, если при ![]() и
и ![]() выполняется неравенство
выполняется неравенство ![]() .
.
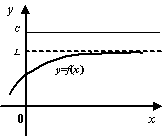
Доказательство этой теоремы достаточно сложно; оно основывается на довольно тонких свойствах системы вещественных чисел, а именно, на том, что у ограниченного снизу множества чисел ![]() , где числа
, где числа ![]() ограничивают функцию
ограничивают функцию ![]() сверху, существует точная нижняя грань
сверху, существует точная нижняя грань ![]() ; она-то и будет пределом неубывающей функции.
; она-то и будет пределом неубывающей функции.
Мы ограничимся здесь этим замечанием и поясняющим рисунком, а за подробным доказательством отошлём читателя к полному курсу математического анализа, например, книгам: Г. М. Фихтенгольц, Курс дифференциального и интегрального исчисления, т. 1 или С. М. Никольский, Курс математического анализа, т. 1.
Имеют место также утверждения, получающиеся из теоремы о пределе монотонной функции сменой знака функции или заменой координаты ![]() :
: