‹-- Назад
Свойства производных
Покажем, что множество функций, имеющих производную в некоторой фиксированной точке ![]() , замкнуто относительно арифметических операций с этими функциями. А именно, докажем следующую теорему, дающую основные правила дифференцирования.
, замкнуто относительно арифметических операций с этими функциями. А именно, докажем следующую теорему, дающую основные правила дифференцирования.
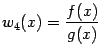 имеют производные в точке
имеют производные в точке Аналогичные утверждения и формулы имеют место также для односторонних производных
Доказательство. Докажем формулу (4.7). Пусть аргументу ![]() дано приращение
дано приращение ![]() ; при этом функция
; при этом функция ![]() получает приращение
получает приращение ![]() , а функция
, а функция ![]() -- приращение
-- приращение ![]() . Их сумма
. Их сумма ![]() получит тогда приращение
получит тогда приращение
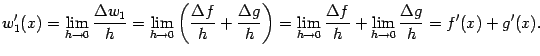
Докажем теперь формулу (4.9). Пусть снова ![]() и
и ![]() -- приращения функций, соответствующие приращению
-- приращения функций, соответствующие приращению ![]() аргумента
аргумента ![]() . Тогда
. Тогда ![]() ,
, ![]() и приращением произведения будет
и приращением произведения будет
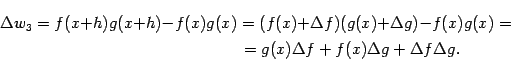
Поэтому, по свойствам пределов,
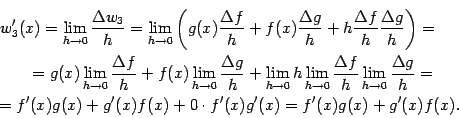
При этом мы вынесли множители
Докажем теперь формулу (4.10). Заметим, что
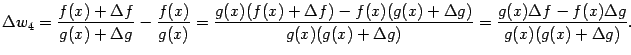
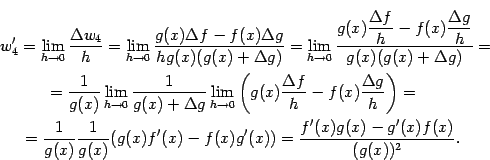
При этом мы вынесли за знак предела постоянный (то есть не зависящий от
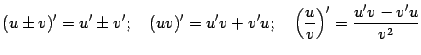 (при
(при
Из этого следствия и формулы (4.7) получается следующее свойство производных: если ![]() и
и ![]() -- постоянные и
-- постоянные и ![]() -- дифференцируемые в точке
-- дифференцируемые в точке ![]() функции, то
функции, то
Если операцию вычисления производной в точке
Поскольку дифференцируемость функции на интервале или отрезке мы определяли как дифференцируемость в каждой точке этого интервала или отрезка, то тем самым мы показали, что операция ![]() перехода от функции
перехода от функции ![]() к её производной
к её производной ![]() ,
, ![]() , также обладает свойством линейности:
, также обладает свойством линейности:
Эти результаты можно выразить ещё и таким образом. Рассмотрим пространство ![]() всех функций
всех функций ![]() , определённых на некотором фиксированном интервале
, определённых на некотором фиксированном интервале ![]() и имеющих производную
и имеющих производную ![]() в точке
в точке ![]() . Тогда операции умножения на постоянные множители и сложения не выводят из этого пространства, то есть пространство
. Тогда операции умножения на постоянные множители и сложения не выводят из этого пространства, то есть пространство ![]() -- это линейное пространство; при этом операция
-- это линейное пространство; при этом операция ![]() -- это линейная операция из пространства
-- это линейная операция из пространства ![]() в линейное пространство вещественных чисел:
в линейное пространство вещественных чисел:
То же верно и для пространств функций, дифференцируемых на интервале ![]() (обозначим это пространство
(обозначим это пространство ![]() ) или на отрезке
) или на отрезке ![]() (обозначим это пространство
(обозначим это пространство ![]() ). Оба этих пространства -- линейные (то есть замкнуты относительно применения к функциям из этих пространств операций сложения и умножения на постоянные), а операция дифференцирования
). Оба этих пространства -- линейные (то есть замкнуты относительно применения к функциям из этих пространств операций сложения и умножения на постоянные), а операция дифференцирования ![]() действует как линейная операция из этих линейных пространств в линейное пространство функций, непрерывных на данном интервале (обозначим это пространство
действует как линейная операция из этих линейных пространств в линейное пространство функций, непрерывных на данном интервале (обозначим это пространство ![]() ; см. предложение 3.4) или отрезке (обозначим это пространство
; см. предложение 3.4) или отрезке (обозначим это пространство ![]() ; также см. предложение 3.4), так как в соответствии с теоремой 4.1 производная каждой дифференцируемой функции
; также см. предложение 3.4), так как в соответствии с теоремой 4.1 производная каждой дифференцируемой функции ![]() -- это непрерывная функция
-- это непрерывная функция ![]() :
: