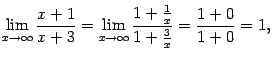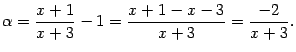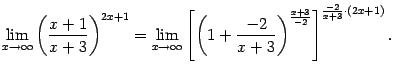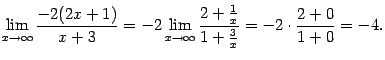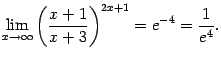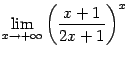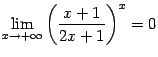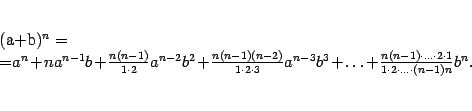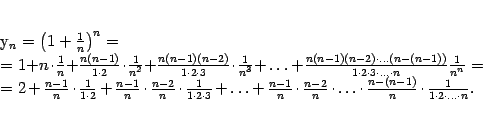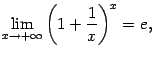‹-- Назад
Первый и второй замечательные пределы
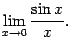
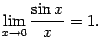
Доказательство. Рассмотрим два односторонних предела 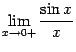 и
и 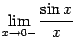 и докажем, что каждый из них равен 1. Тогда по теореме 2.1 двусторонний предел
и докажем, что каждый из них равен 1. Тогда по теореме 2.1 двусторонний предел 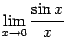 также будет равняться 1.
также будет равняться 1.
Итак, пусть ![]() (этот интервал -- одно из окончаний базы
(этот интервал -- одно из окончаний базы ![]() ). В тригонометрическом круге (радиуса
). В тригонометрическом круге (радиуса ![]() ) с центром
) с центром ![]() построим центральный угол, равный
построим центральный угол, равный ![]() , и проведём вертикальную касательную в точке
, и проведём вертикальную касательную в точке ![]() пересечения горизонтальной оси с окружностью (
пересечения горизонтальной оси с окружностью (![]() ). Обозначим точку пересечения луча с углом наклона
). Обозначим точку пересечения луча с углом наклона ![]() с окружностью буквой
с окружностью буквой ![]() , а с вертикальной касательной -- буквой
, а с вертикальной касательной -- буквой ![]() ; через
; через ![]() обозначим проекцию точки
обозначим проекцию точки ![]() на горизонтальную ось.
на горизонтальную ось.
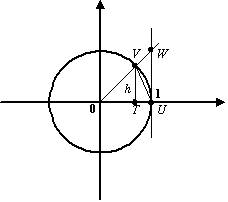
Пусть ![]() -- площадь треугольника
-- площадь треугольника ![]() ,
, ![]() -- площадь кругового сектора
-- площадь кругового сектора ![]() , а
, а ![]() -- площадь треугольника
-- площадь треугольника ![]() . Тогда очевидно следующее неравенство:
. Тогда очевидно следующее неравенство:
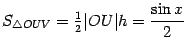 . Площадь центрального сектора круга радиуса
. Площадь центрального сектора круга радиуса 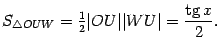 Неравенство, связывающее площади трёх фигур, можно теперь записать в виде
Неравенство, связывающее площади трёх фигур, можно теперь записать в виде 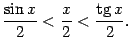
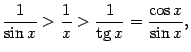
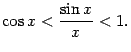
Итак, осталось доказать, что ![]() . Сперва заметим, что
. Сперва заметим, что ![]() , так как
, так как ![]() равняется длине дуги окружности
равняется длине дуги окружности ![]() , которая, очевидно, длиннее хорды
, которая, очевидно, длиннее хорды ![]() . Применяя теорему "о двух милиционерах" к неравенству
. Применяя теорему "о двух милиционерах" к неравенству
Простая замена переменной
Тем самым показано, что
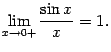
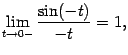
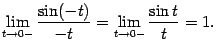
Доказанная теорема означает, что график функции 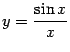 выглядит так:
выглядит так:
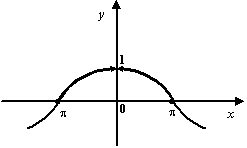
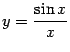
Приведём примеры применения первого замечательного предела для вычисления других родственных пределов.
Очевидно, что
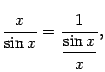
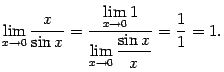
Сделаем замену переменного: пусть ![]() . Тогда
. Тогда ![]() и база
и база ![]() переходит в базу
переходит в базу ![]() . После замены получаем
. После замены получаем
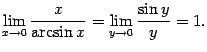
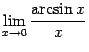 .
. Очевидно, что
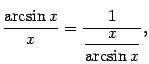
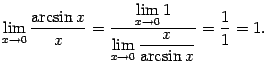
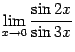 .
. Преобразуем функцию под знаком предела следующим образом:
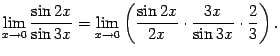
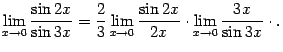
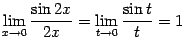
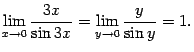
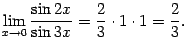
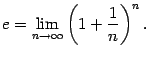
Число ![]() , заданное этим пределом, играет очень большую роль как в математическом анализе, так и в других разделах математики. Число
, заданное этим пределом, играет очень большую роль как в математическом анализе, так и в других разделах математики. Число ![]() часто называют основанием натуральных логарифмов.
часто называют основанием натуральных логарифмов.
Более подробное изучение числа ![]() показывает, что
показывает, что ![]() -- иррациональное число, несколько первых десятичных знаков которого таковы:
-- иррациональное число, несколько первых десятичных знаков которого таковы:
Для доказательства теоремы 2.15 нам понадобится следующая лемма; формула, в ней полученная, называется формулой бинома Ньютона.
Заметим, что в дроби
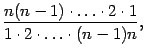
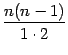 , и т. д. Таким образом, коэффициенты в слагаемых, стоящих на одинаковых местах, считая слева и справа от края формулы, совпадают.
, и т. д. Таким образом, коэффициенты в слагаемых, стоящих на одинаковых местах, считая слева и справа от края формулы, совпадают. Доказательство. Доказывать утверждение леммы будем по индукции по параметру ![]() . При
. При ![]() формула 2.2, очевидно, верна:
формула 2.2, очевидно, верна:
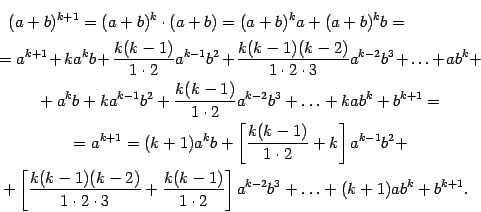
При этом в квадратных скобках получается:
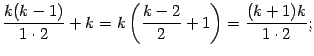 | |
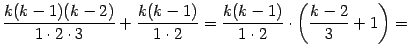 | |
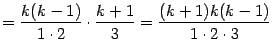 |
и так далее, то есть как раз то, что должно получиться в качестве коэффициентов формулы бинома Ньютона при
Доказательство теоремы 2.15. Рассмотрим последовательность ![]() и применим к
и применим к ![]() формулу бинома Ньютона при
формулу бинома Ньютона при ![]() и
и ![]() . Получим
. Получим
Покажем, что последовательность
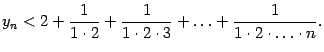
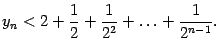
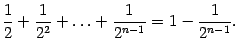
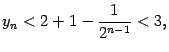
Покажем теперь, что последовательность ![]() не убывает. Действительно, запишем формулу (Доказательство теоремы 2.15) в виде
не убывает. Действительно, запишем формулу (Доказательство теоремы 2.15) в виде
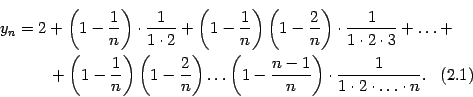
В аналогичной формуле, написанной для
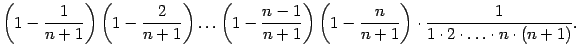
Применим теперь к возрастающей ограниченной сверху последовательности ![]() теорему о пределе монотонной ограниченной функции ( теорема 2.13) и получим, что существует предел
теорему о пределе монотонной ограниченной функции ( теорема 2.13) и получим, что существует предел
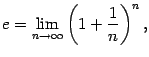
однако строгое доказательство достаточно тяжело, и мы его здесь пропускаем.
В формуле (2.5) можно сделать замену ![]() , при этом база
, при этом база ![]() перейдёт в базу
перейдёт в базу ![]() , и мы получим
, и мы получим
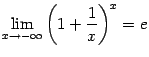
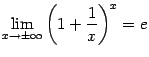
Формулы в этих замечании и упражнении представляют собою другую форму записи второго замечательного предела. Мы сохраним название второй замечательный предел за всеми этими формулами.
Здесь параметр ![]() -- фиксированное число. При вычислении предела он будет рассматриваться как постоянная. Сделаем замену
-- фиксированное число. При вычислении предела он будет рассматриваться как постоянная. Сделаем замену ![]() , тогда
, тогда ![]() и
и ![]() . Поэтому
. Поэтому
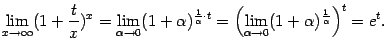
С помощью похожей замены вычисляются пределы функций вида ![]() в случае, когда основание степени
в случае, когда основание степени ![]() при некоторой базе стремится к 1, а показатель степени
при некоторой базе стремится к 1, а показатель степени ![]() -- к бесконечности (то есть является бесконечно большой функцией при данной базе; о бесконечно больших см. ниже, в разделе Бесконечно большие величины и бесконечные пределы). Такие выражения, а также и связанные с ними пределы, называются неопределённостями вида
-- к бесконечности (то есть является бесконечно большой функцией при данной базе; о бесконечно больших см. ниже, в разделе Бесконечно большие величины и бесконечные пределы). Такие выражения, а также и связанные с ними пределы, называются неопределённостями вида ![]() . О неопределённостях других видов пойдёт речь ниже, после примера 2.29.
. О неопределённостях других видов пойдёт речь ниже, после примера 2.29.
Обратим внимание читателя, что ![]() -- это лишь условная запись: 1 здесь указывает, что основание степени стремится к 1 (и вовсе не обязательно равно 1); в "показателе степени" стоит вообще не число, а символ бесконечности. Поэтому было бы грубой ошибкой, встретив такую условную запись (или написав её), сделать вывод о том, что единица, мол, в любой степени даёт единицу, и поэтому ответ равен единице. С условными символами в этой записи нельзя действовать так же, как с числами. Предыдущий пример, в котором основание степени
-- это лишь условная запись: 1 здесь указывает, что основание степени стремится к 1 (и вовсе не обязательно равно 1); в "показателе степени" стоит вообще не число, а символ бесконечности. Поэтому было бы грубой ошибкой, встретив такую условную запись (или написав её), сделать вывод о том, что единица, мол, в любой степени даёт единицу, и поэтому ответ равен единице. С условными символами в этой записи нельзя действовать так же, как с числами. Предыдущий пример, в котором основание степени ![]() стремится к 1, а показатель степени
стремится к 1, а показатель степени ![]() к
к ![]() , даёт как раз неопределённость вида
, даёт как раз неопределённость вида ![]() . Однако значение предела равно
. Однако значение предела равно ![]() , а этот результат может быть любым положительным числом, в зависимости от того, какое значение
, а этот результат может быть любым положительным числом, в зависимости от того, какое значение ![]() взято.
взято.
Вот ещё один пример на раскрытие неопределённости вида ![]() .
.
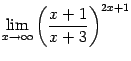 .
. Здесь основание степени имеет предел